Grounding FO and FO(ID) with Bounds

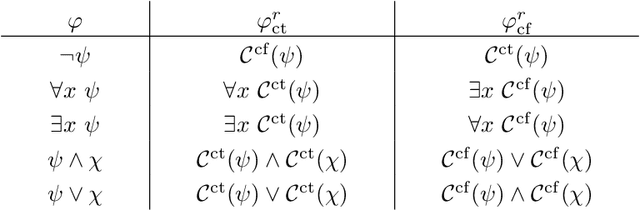
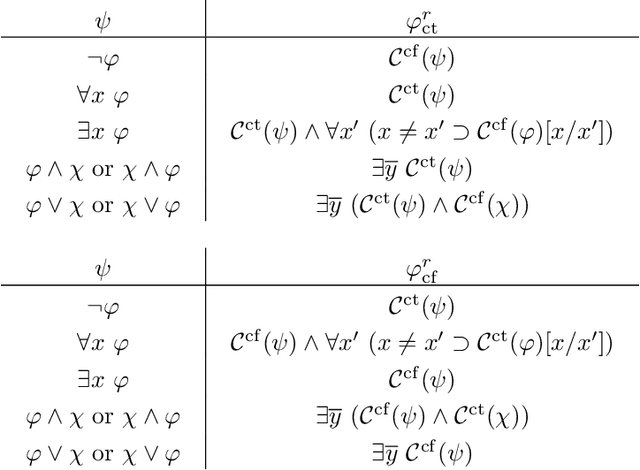
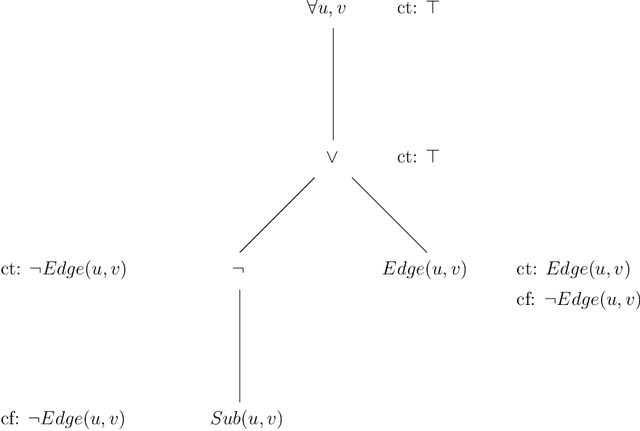
Grounding is the task of reducing a first-order theory and finite domain to an equivalent propositional theory. It is used as preprocessing phase in many logic-based reasoning systems. Such systems provide a rich first-order input language to a user and can rely on efficient propositional solvers to perform the actual reasoning. Besides a first-order theory and finite domain, the input for grounders contains in many applications also additional data. By exploiting this data, the size of the grounders output can often be reduced significantly. A common practice to improve the efficiency of a grounder in this context is by manually adding semantically redundant information to the input theory, indicating where and when the grounder should exploit the data. In this paper we present a method to compute and add such redundant information automatically. Our method therefore simplifies the task of writing input theories that can be grounded efficiently by current systems. We first present our method for classical first-order logic (FO) theories. Then we extend it to FO(ID), the extension of FO with inductive definitions, which allows for more concise and comprehensive input theories. We discuss implementation issues and experimentally validate the practical applicability of our method.

Lifted Unit Propagation for Effective Grounding

A grounding of a formula $\phi$ over a given finite domain is a ground formula which is equivalent to $\phi$ on that domain. Very effective propositional solvers have made grounding-based methods for problem solving increasingly important, however for realistic problem domains and instances, the size of groundings is often problematic. A key technique in ground (e.g., SAT) solvers is unit propagation, which often significantly reduces ground formula size even before search begins. We define a "lifted" version of unit propagation which may be carried out prior to grounding, and describe integration of the resulting technique into grounding algorithms. We describe an implementation of the method in a bottom-up grounder, and an experimental study of its performance.