CP-logic: A Language of Causal Probabilistic Events and Its Relation to Logic Programming
Paper and Code
Apr 10, 2009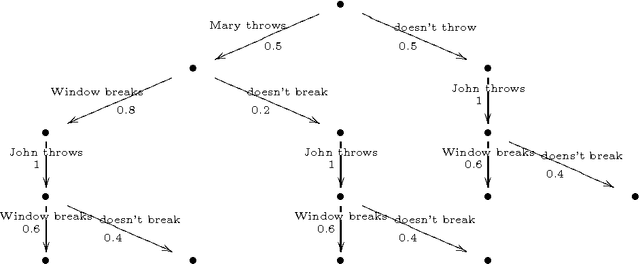
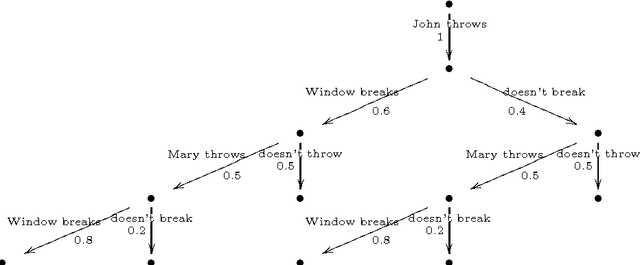
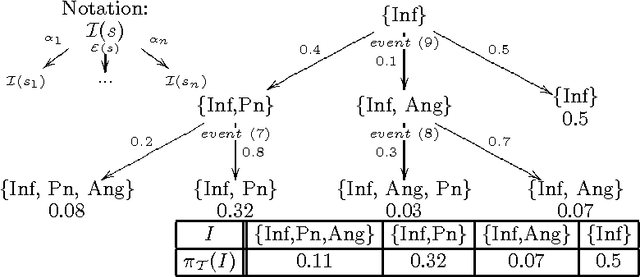

This papers develops a logical language for representing probabilistic causal laws. Our interest in such a language is twofold. First, it can be motivated as a fundamental study of the representation of causal knowledge. Causality has an inherent dynamic aspect, which has been studied at the semantical level by Shafer in his framework of probability trees. In such a dynamic context, where the evolution of a domain over time is considered, the idea of a causal law as something which guides this evolution is quite natural. In our formalization, a set of probabilistic causal laws can be used to represent a class of probability trees in a concise, flexible and modular way. In this way, our work extends Shafer's by offering a convenient logical representation for his semantical objects. Second, this language also has relevance for the area of probabilistic logic programming. In particular, we prove that the formal semantics of a theory in our language can be equivalently defined as a probability distribution over the well-founded models of certain logic programs, rendering it formally quite similar to existing languages such as ICL or PRISM. Because we can motivate and explain our language in a completely self-contained way as a representation of probabilistic causal laws, this provides a new way of explaining the intuitions behind such probabilistic logic programs: we can say precisely which knowledge such a program expresses, in terms that are equally understandable by a non-logician. Moreover, we also obtain an additional piece of knowledge representation methodology for probabilistic logic programs, by showing how they can express probabilistic causal laws.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge