Knowledge Authoring for Rules and Actions

Knowledge representation and reasoning (KRR) systems describe and reason with complex concepts and relations in the form of facts and rules. Unfortunately, wide deployment of KRR systems runs into the problem that domain experts have great difficulty constructing correct logical representations of their domain knowledge. Knowledge engineers can help with this construction process, but there is a deficit of such specialists. The earlier Knowledge Authoring Logic Machine (KALM) based on Controlled Natural Language (CNL) was shown to have very high accuracy for authoring facts and questions. More recently, KALMFL, a successor of KALM, replaced CNL with factual English, which is much less restrictive and requires very little training from users. However, KALMFL has limitations in representing certain types of knowledge, such as authoring rules for multi-step reasoning or understanding actions with timestamps. To address these limitations, we propose KALMRA to enable authoring of rules and actions. Our evaluation using the UTI guidelines benchmark shows that KALMRA achieves a high level of correctness (100%) on rule authoring. When used for authoring and reasoning with actions, KALMRA achieves more than 99.3% correctness on the bAbI benchmark, demonstrating its effectiveness in more sophisticated KRR jobs. Finally, we illustrate the logical reasoning capabilities of KALMRA by drawing attention to the problems faced by the recently made famous AI, ChatGPT.

MLRegTest: A Benchmark for the Machine Learning of Regular Languages

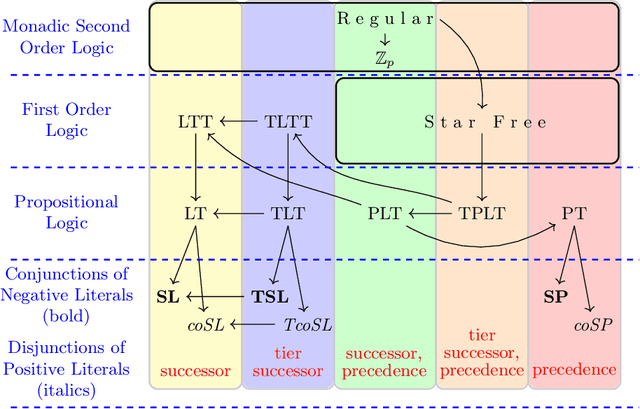
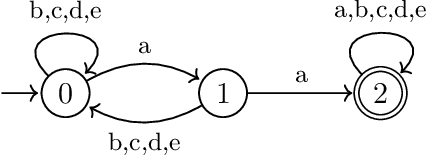
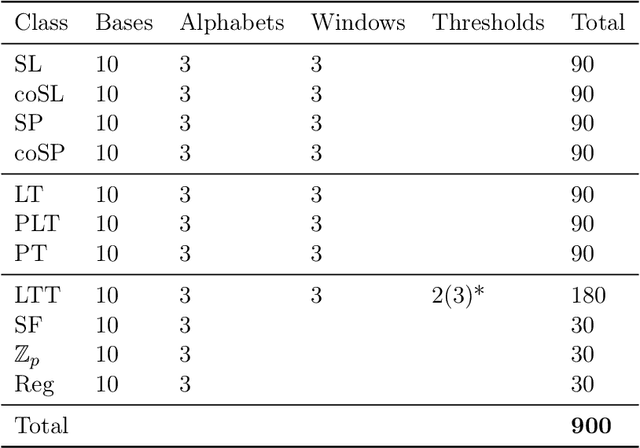
Evaluating machine learning (ML) systems on their ability to learn known classifiers allows fine-grained examination of the patterns they can learn, which builds confidence when they are applied to the learning of unknown classifiers. This article presents a new benchmark for ML systems on sequence classification called MLRegTest, which contains training, development, and test sets from 1,800 regular languages. Different kinds of formal languages represent different kinds of long-distance dependencies, and correctly identifying long-distance dependencies in sequences is a known challenge for ML systems to generalize successfully. MLRegTest organizes its languages according to their logical complexity (monadic second order, first order, propositional, or monomial expressions) and the kind of logical literals (string, tier-string, subsequence, or combinations thereof). The logical complexity and choice of literal provides a systematic way to understand different kinds of long-distance dependencies in regular languages, and therefore to understand the capacities of different ML systems to learn such long-distance dependencies. Finally, the performance of different neural networks (simple RNN, LSTM, GRU, transformer) on MLRegTest is examined. The main conclusion is that their performance depends significantly on the kind of test set, the class of language, and the neural network architecture.

Knowledge Authoring with Factual English

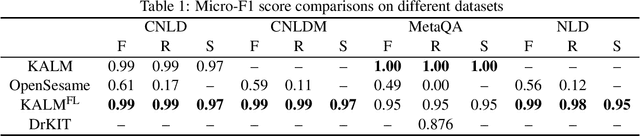
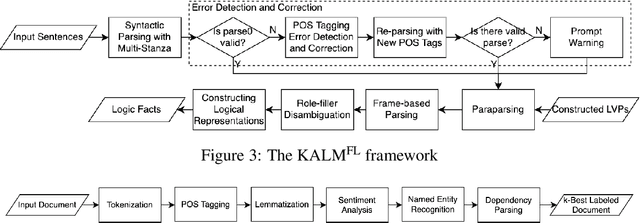
Knowledge representation and reasoning (KRR) systems represent knowledge as collections of facts and rules. Like databases, KRR systems contain information about domains of human activities like industrial enterprises, science, and business. KRRs can represent complex concepts and relations, and they can query and manipulate information in sophisticated ways. Unfortunately, the KRR technology has been hindered by the fact that specifying the requisite knowledge requires skills that most domain experts do not have, and professional knowledge engineers are hard to find. One solution could be to extract knowledge from English text, and a number of works have attempted to do so (OpenSesame, Google's Sling, etc.). Unfortunately, at present, extraction of logical facts from unrestricted natural language is still too inaccurate to be used for reasoning, while restricting the grammar of the language (so-called controlled natural language, or CNL) is hard for the users to learn and use. Nevertheless, some recent CNL-based approaches, such as the Knowledge Authoring Logic Machine (KALM), have shown to have very high accuracy compared to others, and a natural question is to what extent the CNL restrictions can be lifted. In this paper, we address this issue by transplanting the KALM framework to a neural natural language parser, mStanza. Here we limit our attention to authoring facts and queries and therefore our focus is what we call factual English statements. Authoring other types of knowledge, such as rules, will be considered in our followup work. As it turns out, neural network based parsers have problems of their own and the mistakes they make range from part-of-speech tagging to lemmatization to dependency errors. We present a number of techniques for combating these problems and test the new system, KALMFL (i.e., KALM for factual language), on a number of benchmarks, which show KALMFL achieves correctness in excess of 95%.

Proceedings 37th International Conference on Logic Programming (Technical Communications)

ICLP is the premier international event for presenting research in logic programming. Contributions to ICLP 2021 were sought in all areas of logic programming, including but not limited to: Foundations: Semantics, Formalisms, Nonmonotonic reasoning, Knowledge representation. Languages issues: Concurrency, Objects, Coordination, Mobility, Higher order, Types, Modes, Assertions, Modules, Meta-programming, Logic-based domain-specific languages, Programming techniques. Programming support: Program analysis, Transformation, Validation, Verification, Debugging, Profiling, Testing, Execution visualization. Implementation: Compilation, Virtual machines, Memory management, Parallel and Distributed execution, Constraint handling rules, Tabling, Foreign interfaces, User interfaces. Related Paradigms and Synergies: Inductive and coinductive logic programming, Constraint logic programming, Answer set programming, Interaction with SAT, SMT and CSP solvers, Theorem proving, Argumentation, Probabilistic programming, Machine learning. Applications: Databases, Big data, Data integration and federation, Software engineering, Natural language processing, Web and semantic web, Agents, Artificial intelligence, Computational life sciences, Cyber-security, Robotics, Education.

Proceedings 36th International Conference on Logic Programming (Technical Communications)

Since the first conference held in Marseille in 1982, ICLP has been the premier international event for presenting research in logic programming. Contributions are solicited in all areas of logic programming and related areas, including but not restricted to: - Foundations: Semantics, Formalisms, Answer-Set Programming, Non-monotonic Reasoning, Knowledge Representation. - Declarative Programming: Inference engines, Analysis, Type and mode inference, Partial evaluation, Abstract interpretation, Transformation, Validation, Verification, Debugging, Profiling, Testing, Logic-based domain-specific languages, constraint handling rules. - Related Paradigms and Synergies: Inductive and Co-inductive Logic Programming, Constraint Logic Programming, Interaction with SAT, SMT and CSP solvers, Logic programming techniques for type inference and theorem proving, Argumentation, Probabilistic Logic Programming, Relations to object-oriented and Functional programming, Description logics, Neural-Symbolic Machine Learning, Hybrid Deep Learning and Symbolic Reasoning. - Implementation: Concurrency and distribution, Objects, Coordination, Mobility, Virtual machines, Compilation, Higher Order, Type systems, Modules, Constraint handling rules, Meta-programming, Foreign interfaces, User interfaces. - Applications: Databases, Big Data, Data Integration and Federation, Software Engineering, Natural Language Processing, Web and Semantic Web, Agents, Artificial Intelligence, Bioinformatics, Education, Computational life sciences, Education, Cybersecurity, and Robotics.

Proceedings 35th International Conference on Logic Programming (Technical Communications)

Since the first conference held in Marseille in 1982, ICLP has been the premier international event for presenting research in logic programming. Contributions are sought in all areas of logic programming, including but not restricted to: Foundations: Semantics, Formalisms, Nonmonotonic reasoning, Knowledge representation. Languages: Concurrency, Objects, Coordination, Mobility, Higher Order, Types, Modes, Assertions, Modules, Meta-programming, Logic-based domain-specific languages, Programming Techniques. Declarative programming: Declarative program development, Analysis, Type and mode inference, Partial evaluation, Abstract interpretation, Transformation, Validation, Verification, Debugging, Profiling, Testing, Execution visualization Implementation: Virtual machines, Compilation, Memory management, Parallel/distributed execution, Constraint handling rules, Tabling, Foreign interfaces, User interfaces. Related Paradigms and Synergies: Inductive and Co-inductive Logic Programming, Constraint Logic Programming, Answer Set Programming, Interaction with SAT, SMT and CSP solvers, Logic programming techniques for type inference and theorem proving, Argumentation, Probabilistic Logic Programming, Relations to object-oriented and Functional programming. Applications: Databases, Big Data, Data integration and federation, Software engineering, Natural language processing, Web and Semantic Web, Agents, Artificial intelligence, Computational life sciences, Education, Cybersecurity, and Robotics.

Querying Knowledge via Multi-Hop English Questions

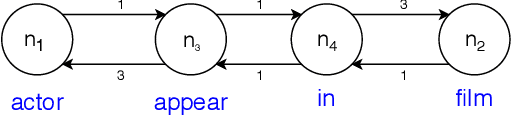
The inherent difficulty of knowledge specification and the lack of trained specialists are some of the key obstacles on the way to making intelligent systems based on the knowledge representation and reasoning (KRR) paradigm commonplace. Knowledge and query authoring using natural language, especially controlled natural language (CNL), is one of the promising approaches that could enable domain experts, who are not trained logicians, to both create formal knowledge and query it. In previous work, we introduced the KALM system (Knowledge Authoring Logic Machine) that supports knowledge authoring (and simple querying) with very high accuracy that at present is unachievable via machine learning approaches. The present paper expands on the question answering aspect of KALM and introduces KALM-QA (KALM for Question Answering) that is capable of answering much more complex English questions. We show that KALM-QA achieves 100% accuracy on an extensive suite of movie-related questions, called MetaQA, which contains almost 29,000 test questions and over 260,000 training questions. We contrast this with a published machine learning approach, which falls far short of this high mark.

Paraconsistency and Word Puzzles

Word puzzles and the problem of their representations in logic languages have received considerable attention in the last decade (Ponnuru et al. 2004; Shapiro 2011; Baral and Dzifcak 2012; Schwitter 2013). Of special interest is the problem of generating such representations directly from natural language (NL) or controlled natural language (CNL). An interesting variation of this problem, and to the best of our knowledge, scarcely explored variation in this context, is when the input information is inconsistent. In such situations, the existing encodings of word puzzles produce inconsistent representations and break down. In this paper, we bring the well-known type of paraconsistent logics, called Annotated Predicate Calculus (APC) (Kifer and Lozinskii 1992), to bear on the problem. We introduce a new kind of non-monotonic semantics for APC, called consistency preferred stable models and argue that it makes APC into a suitable platform for dealing with inconsistency in word puzzles and, more generally, in NL sentences. We also devise a number of general principles to help the user choose among the different representations of NL sentences, which might seem equivalent but, in fact, behave differently when inconsistent information is taken into account. These principles can be incorporated into existing CNL translators, such as Attempto Controlled English (ACE) (Fuchs et al. 2008) and PENG Light (White and Schwitter 2009). Finally, we show that APC with the consistency preferred stable model semantics can be equivalently embedded in ASP with preferences over stable models, and we use this embedding to implement this version of APC in Clingo (Gebser et al. 2011) and its Asprin add-on (Brewka et al. 2015).

Initial Results on the F-logic to OWL Bi-directional Translation on a Tabled Prolog Engine

In this paper, we show our results on the bi-directional data exchange between the F-logic language supported by the Flora2 system and the OWL language. Most of the TBox and ABox axioms are translated preserving the semantics between the two representations, such as: proper inclusion, individual definition, functional properties, while some axioms and restrictions require a change in the semantics, such as: numbered and qualified cardinality restrictions. For the second case, we translate the OWL definite style inference rules into F-logic style constraints. We also describe a set of reasoning examples using the above translation, including the reasoning in Flora2 of a variety of ABox queries.

Efficient Tabling Mechanisms for Transaction Logic Programs

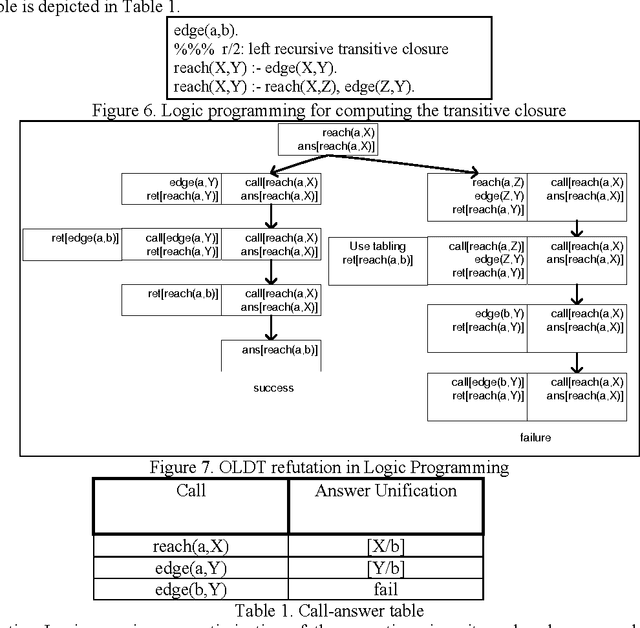
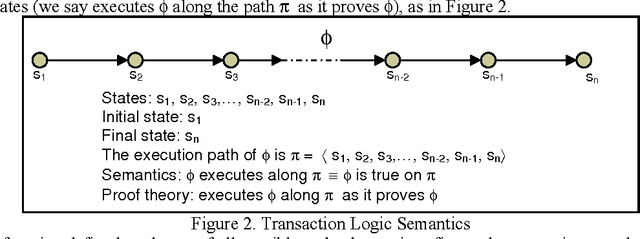
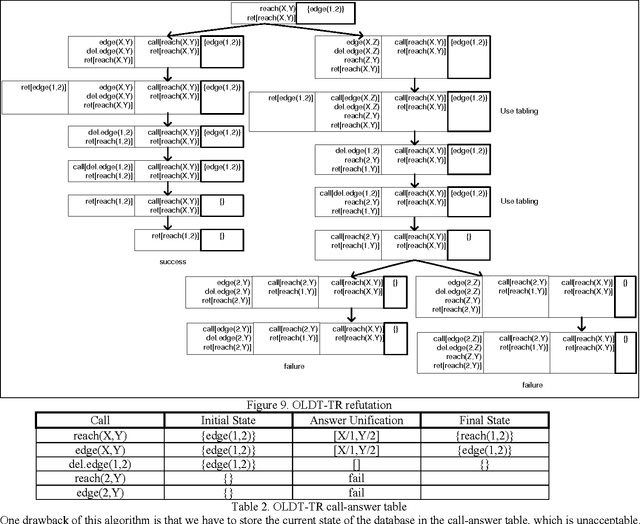
In this paper we present efficient evaluation algorithms for the Horn Transaction Logic (a generalization of the regular Horn logic programs with state updates). We present two complementary methods for optimizing the implementation of Transaction Logic. The first method is based on tabling and we modified the proof theory to table calls and answers on states (practically, equivalent to dynamic programming). The call-answer table is indexed on the call and a signature of the state in which the call was made. The answer columns contain the answer unification and a signature of the state after the call was executed. The states are signed efficiently using a technique based on tries and counting. The second method is based on incremental evaluation and it applies when the data oracle contains derived relations. The deletions and insertions (executed in the transaction oracle) change the state of the database. Using the heuristic of inertia (only a part of the state changes in response to elementary updates), most of the time it is cheaper to compute only the changes in the state than to recompute the entire state from scratch. The two methods are complementary by the fact that the first method optimizes the evaluation when a call is repeated in the same state, and the second method optimizes the evaluation of a new state when a call-state pair is not found by the tabling mechanism (i.e. the first method). The proof theory of Transaction Logic with the application of tabling and incremental evaluation is sound and complete with respect to its model theory.