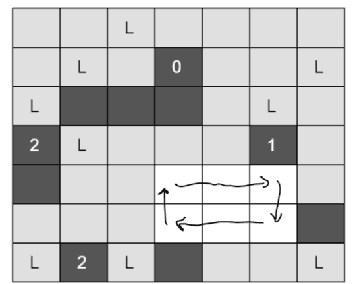
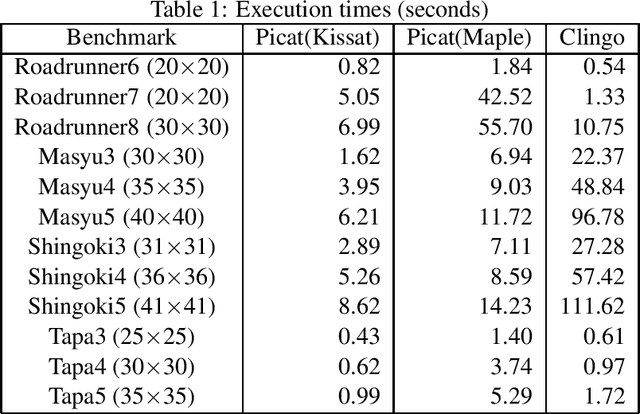
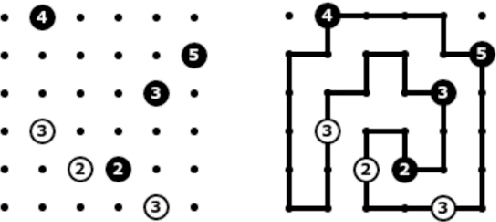
Modeling and Solving Graph Synthesis Problems Using SAT-Encoded Reachability Constraints in Picat

Many constraint satisfaction problems involve synthesizing subgraphs that satisfy certain reachability constraints. This paper presents programs in Picat for four problems selected from the recent LP/CP programming competitions. The programs demonstrate the modeling capabilities of the Picat language and the solving efficiency of the cutting-edge SAT solvers empowered with effective encodings.

Proceedings 37th International Conference on Logic Programming (Technical Communications)

ICLP is the premier international event for presenting research in logic programming. Contributions to ICLP 2021 were sought in all areas of logic programming, including but not limited to: Foundations: Semantics, Formalisms, Nonmonotonic reasoning, Knowledge representation. Languages issues: Concurrency, Objects, Coordination, Mobility, Higher order, Types, Modes, Assertions, Modules, Meta-programming, Logic-based domain-specific languages, Programming techniques. Programming support: Program analysis, Transformation, Validation, Verification, Debugging, Profiling, Testing, Execution visualization. Implementation: Compilation, Virtual machines, Memory management, Parallel and Distributed execution, Constraint handling rules, Tabling, Foreign interfaces, User interfaces. Related Paradigms and Synergies: Inductive and coinductive logic programming, Constraint logic programming, Answer set programming, Interaction with SAT, SMT and CSP solvers, Theorem proving, Argumentation, Probabilistic programming, Machine learning. Applications: Databases, Big data, Data integration and federation, Software engineering, Natural language processing, Web and semantic web, Agents, Artificial intelligence, Computational life sciences, Cyber-security, Robotics, Education.

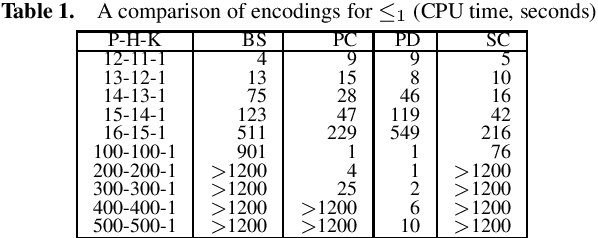
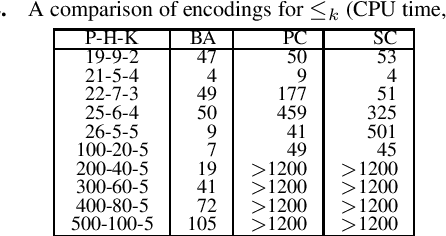
Yet Another Comparison of SAT Encodings for the At-Most-K Constraint

The at-most-k constraint is ubiquitous in combinatorial problems, and numerous SAT encodings are available for the constraint. Prior experiments have shown the competitiveness of the sequential-counter encoding for k $>$ 1, and have excluded the parallel-counter encoding, which is more compact that the binary-adder encoding, from consideration due to its incapability of enforcing arc consistency through unit propagation. This paper presents an experiment that shows astounding performance of the binary-adder encoding for the at-most-k constraint.

Planning as Tabled Logic Programming

This paper describes Picat's planner, its implementation, and planning models for several domains used in International Planning Competition (IPC) 2014. Picat's planner is implemented by use of tabling. During search, every state encountered is tabled, and tabled states are used to effectively perform resource-bounded search. In Picat, structured data can be used to avoid enumerating all possible permutations of objects, and term sharing is used to avoid duplication of common state data. This paper presents several modeling techniques through the example models, ranging from designing state representations to facilitate data sharing and symmetry breaking, encoding actions with operations for efficient precondition checking and state updating, to incorporating domain knowledge and heuristics. Broadly, this paper demonstrates the effectiveness of tabled logic programming for planning, and argues the importance of modeling despite recent significant progress in domain-independent PDDL planners.

Using Tabled Logic Programming to Solve the Petrobras Planning Problem

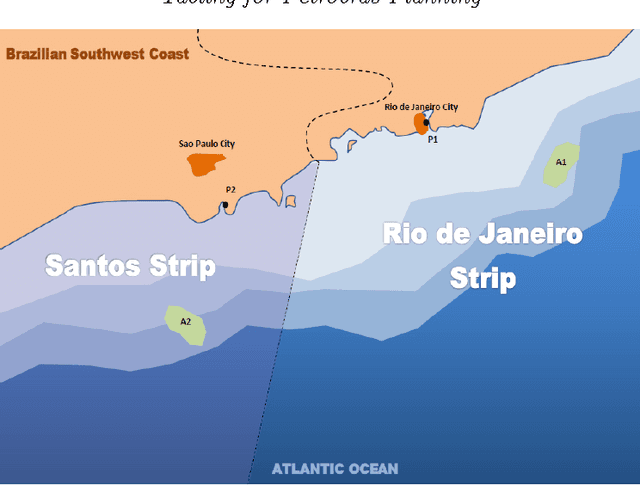
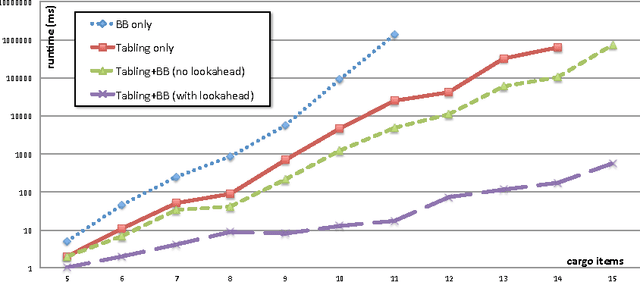
Tabling has been used for some time to improve efficiency of Prolog programs by memorizing answered queries. The same idea can be naturally used to memorize visited states during search for planning. In this paper we present a planner developed in the Picat language to solve the Petrobras planning problem. Picat is a novel Prolog-like language that provides pattern matching, deterministic and non-deterministic rules, and tabling as its core modelling and solving features. We demonstrate these capabilities using the Petrobras problem, where the goal is to plan transport of cargo items from ports to platforms using vessels with limited capacity. Monte Carlo Tree Search has been so far the best technique to tackle this problem and we will show that by using tabling we can achieve much better runtime efficiency and better plan quality.

Toward a Dynamic Programming Solution for the 4-peg Tower of Hanoi Problem with Configurations

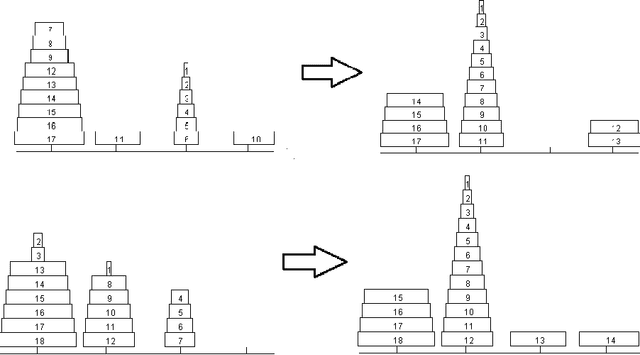
The Frame-Stewart algorithm for the 4-peg variant of the Tower of Hanoi, introduced in 1941, partitions disks into intermediate towers before moving the remaining disks to their destination. Algorithms that partition the disks have not been proven to be optimal, although they have been verified for up to 30 disks. This paper presents a dynamic programming approach to this algorithm, using tabling in B-Prolog. This study uses a variation of the problem, involving configurations of disks, in order to contrast the tabling approach with the approaches utilized by other solvers. A comparison of different partitioning locations for the Frame-Stewart algorithm indicates that, although certain partitions are optimal for the classic problem, they need to be modified for certain configurations, and that random configurations might require an entirely new algorithm.

Linear Tabulated Resolution Based on Prolog Control Strategy

Infinite loops and redundant computations are long recognized open problems in Prolog. Two ways have been explored to resolve these problems: loop checking and tabling. Loop checking can cut infinite loops, but it cannot be both sound and complete even for function-free logic programs. Tabling seems to be an effective way to resolve infinite loops and redundant computations. However, existing tabulated resolutions, such as OLDT-resolution, SLG- resolution, and Tabulated SLS-resolution, are non-linear because they rely on the solution-lookup mode in formulating tabling. The principal disadvantage of non-linear resolutions is that they cannot be implemented using a simple stack-based memory structure like that in Prolog. Moreover, some strictly sequential operators such as cuts may not be handled as easily as in Prolog. In this paper, we propose a hybrid method to resolve infinite loops and redundant computations. We combine the ideas of loop checking and tabling to establish a linear tabulated resolution called TP-resolution. TP-resolution has two distinctive features: (1) It makes linear tabulated derivations in the same way as Prolog except that infinite loops are broken and redundant computations are reduced. It handles cuts as effectively as Prolog. (2) It is sound and complete for positive logic programs with the bounded-term-size property. The underlying algorithm can be implemented by an extension to any existing Prolog abstract machines such as WAM or ATOAM.