Characterizations of Stable Model Semantics for Logic Programs with Arbitrary Constraint Atoms

This paper studies the stable model semantics of logic programs with (abstract) constraint atoms and their properties. We introduce a succinct abstract representation of these constraint atoms in which a constraint atom is represented compactly. We show two applications. First, under this representation of constraint atoms, we generalize the Gelfond-Lifschitz transformation and apply it to define stable models (also called answer sets) for logic programs with arbitrary constraint atoms. The resulting semantics turns out to coincide with the one defined by Son et al., which is based on a fixpoint approach. One advantage of our approach is that it can be applied, in a natural way, to define stable models for disjunctive logic programs with constraint atoms, which may appear in the disjunctive head as well as in the body of a rule. As a result, our approach to the stable model semantics for logic programs with constraint atoms generalizes a number of previous approaches. Second, we show that our abstract representation of constraint atoms provides a means to characterize dependencies of atoms in a program with constraint atoms, so that some standard characterizations and properties relying on these dependencies in the past for logic programs with ordinary atoms can be extended to logic programs with constraint atoms.

Enhancing Global SLS-Resolution with Loop Cutting and Tabling Mechanisms

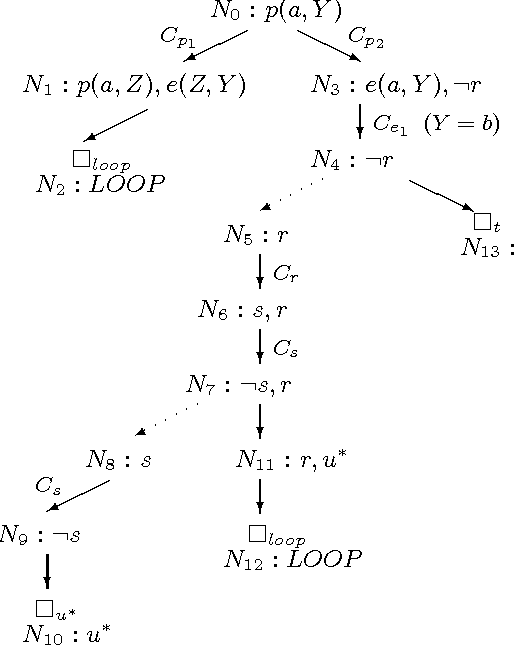
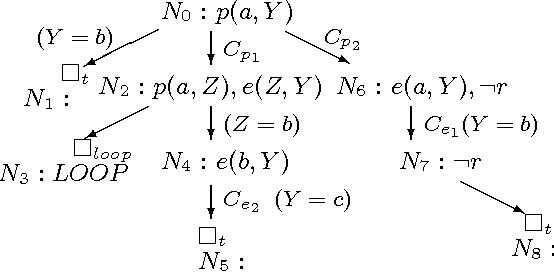
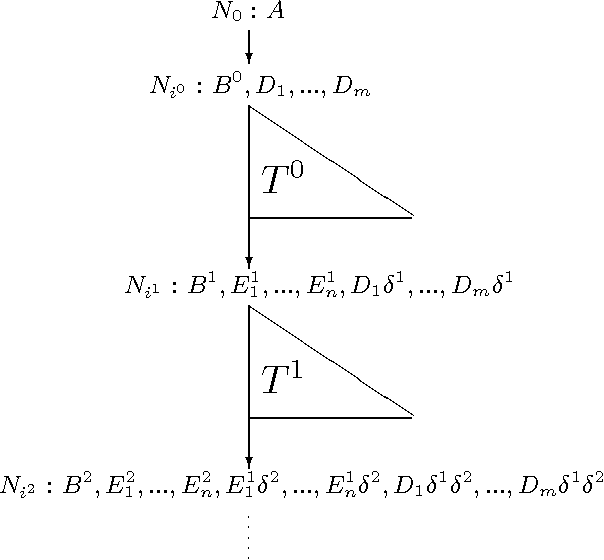
Global SLS-resolution is a well-known procedural semantics for top-down computation of queries under the well-founded model. It inherits from SLDNF-resolution the {\em linearity} property of derivations, which makes it easy and efficient to implement using a simple stack-based memory structure. However, like SLDNF-resolution it suffers from the problem of infinite loops and redundant computations. To resolve this problem, in this paper we develop a new procedural semantics, called {\em SLTNF-resolution}, by enhancing Global SLS-resolution with loop cutting and tabling mechanisms. SLTNF-resolution is sound and complete w.r.t. the well-founded semantics for logic programs with the bounded-term-size property, and is superior to existing linear tabling procedural semantics such as SLT-resolution.

SLT-Resolution for the Well-Founded Semantics

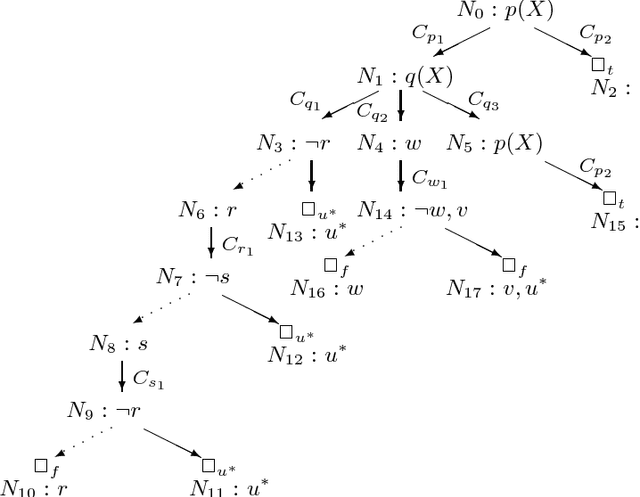
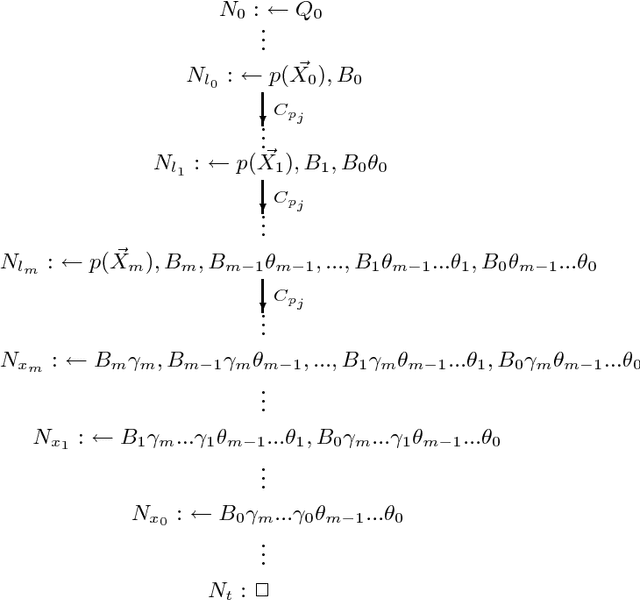
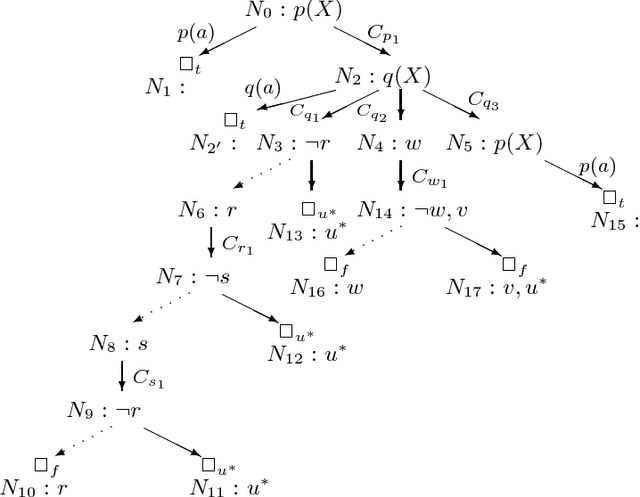
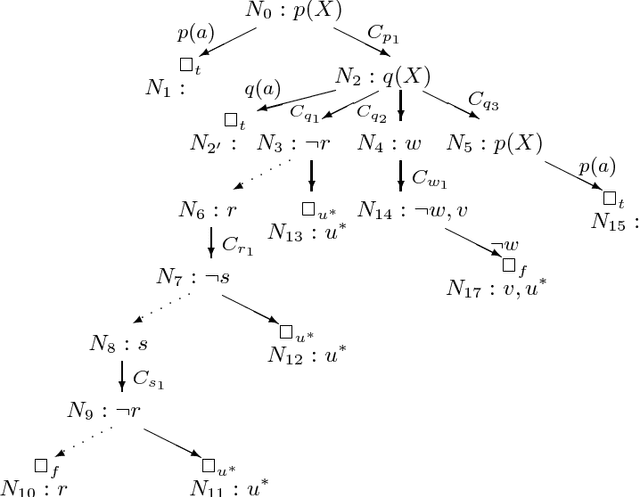
Global SLS-resolution and SLG-resolution are two representative mechanisms for top-down evaluation of the well-founded semantics of general logic programs. Global SLS-resolution is linear for query evaluation but suffers from infinite loops and redundant computations. In contrast, SLG-resolution resolves infinite loops and redundant computations by means of tabling, but it is not linear. The principal disadvantage of a non-linear approach is that it cannot be implemented using a simple, efficient stack-based memory structure nor can it be easily extended to handle some strictly sequential operators such as cuts in Prolog. In this paper, we present a linear tabling method, called SLT-resolution, for top-down evaluation of the well-founded semantics. SLT-resolution is a substantial extension of SLDNF-resolution with tabling. Its main features include: (1) It resolves infinite loops and redundant computations while preserving the linearity. (2) It is terminating, and sound and complete w.r.t. the well-founded semantics for programs with the bounded-term-size property with non-floundering queries. Its time complexity is comparable with SLG-resolution and polynomial for function-free logic programs. (3) Because of its linearity for query evaluation, SLT-resolution bridges the gap between the well-founded semantics and standard Prolog implementation techniques. It can be implemented by an extension to any existing Prolog abstract machines such as WAM or ATOAM.

Verifying Termination of General Logic Programs with Concrete Queries

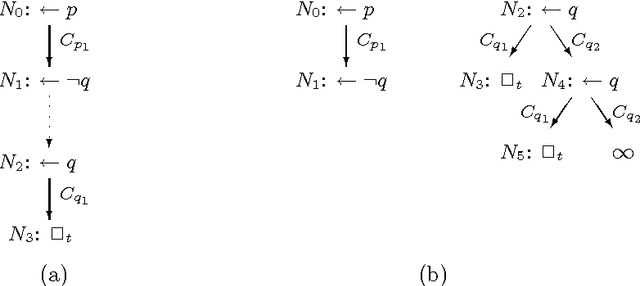
We introduce a method of verifying termination of logic programs with respect to concrete queries (instead of abstract query patterns). A necessary and sufficient condition is established and an algorithm for automatic verification is developed. In contrast to existing query pattern-based approaches, our method has the following features: (1) It applies to all general logic programs with non-floundering queries. (2) It is very easy to automate because it does not need to search for a level mapping or a model, nor does it need to compute an interargument relation based on additional mode or type information. (3) It bridges termination analysis with loop checking, the two problems that have been studied separately in the past despite their close technical relation with each other.

Linear Tabulated Resolution Based on Prolog Control Strategy

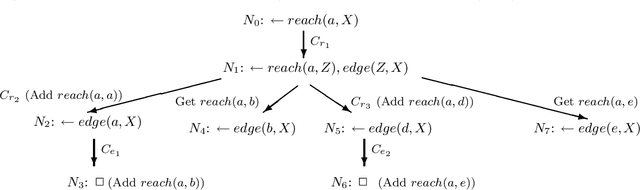
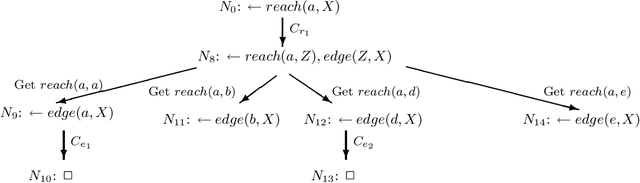
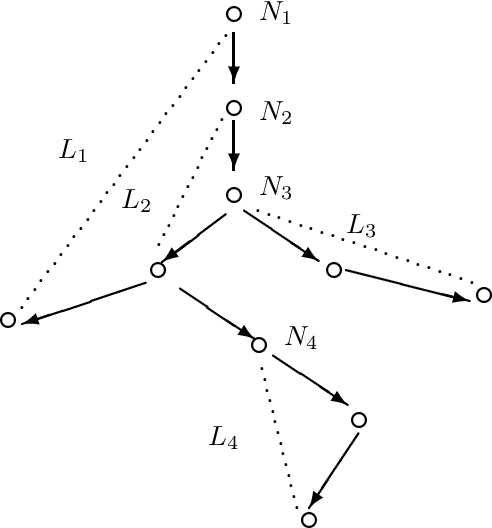
Infinite loops and redundant computations are long recognized open problems in Prolog. Two ways have been explored to resolve these problems: loop checking and tabling. Loop checking can cut infinite loops, but it cannot be both sound and complete even for function-free logic programs. Tabling seems to be an effective way to resolve infinite loops and redundant computations. However, existing tabulated resolutions, such as OLDT-resolution, SLG- resolution, and Tabulated SLS-resolution, are non-linear because they rely on the solution-lookup mode in formulating tabling. The principal disadvantage of non-linear resolutions is that they cannot be implemented using a simple stack-based memory structure like that in Prolog. Moreover, some strictly sequential operators such as cuts may not be handled as easily as in Prolog. In this paper, we propose a hybrid method to resolve infinite loops and redundant computations. We combine the ideas of loop checking and tabling to establish a linear tabulated resolution called TP-resolution. TP-resolution has two distinctive features: (1) It makes linear tabulated derivations in the same way as Prolog except that infinite loops are broken and redundant computations are reduced. It handles cuts as effectively as Prolog. (2) It is sound and complete for positive logic programs with the bounded-term-size property. The underlying algorithm can be implemented by an extension to any existing Prolog abstract machines such as WAM or ATOAM.