Multi-Agent Pathfinding: Definitions, Variants, and Benchmarks

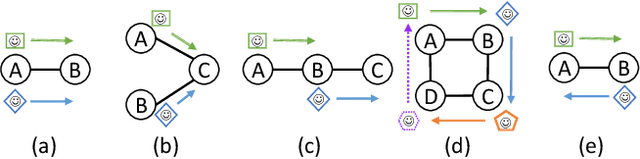
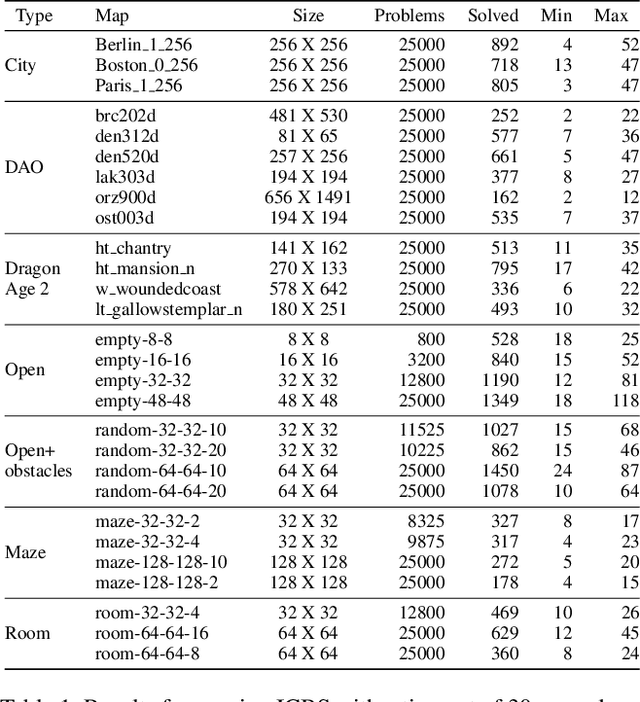
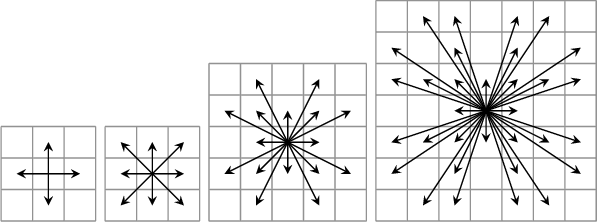
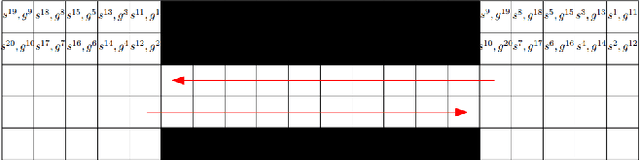
The MAPF problem is the fundamental problem of planning paths for multiple agents, where the key constraint is that the agents will be able to follow these paths concurrently without colliding with each other. Applications of MAPF include automated warehouses and autonomous vehicles. Research on MAPF has been flourishing in the past couple of years. Different MAPF research papers make different assumptions, e.g., whether agents can traverse the same road at the same time, and have different objective functions, e.g., minimize makespan or sum of agents' actions costs. These assumptions and objectives are sometimes implicitly assumed or described informally. This makes it difficult to establish appropriate baselines for comparison in research papers, as well as making it difficult for practitioners to find the papers relevant to their concrete application. This paper aims to fill this gap and support researchers and practitioners by providing a unifying terminology for describing common MAPF assumptions and objectives. In addition, we also provide pointers to two MAPF benchmarks. In particular, we introduce a new grid-based benchmark for MAPF, and demonstrate experimentally that it poses a challenge to contemporary MAPF algorithms.

Planning as Tabled Logic Programming

This paper describes Picat's planner, its implementation, and planning models for several domains used in International Planning Competition (IPC) 2014. Picat's planner is implemented by use of tabling. During search, every state encountered is tabled, and tabled states are used to effectively perform resource-bounded search. In Picat, structured data can be used to avoid enumerating all possible permutations of objects, and term sharing is used to avoid duplication of common state data. This paper presents several modeling techniques through the example models, ranging from designing state representations to facilitate data sharing and symmetry breaking, encoding actions with operations for efficient precondition checking and state updating, to incorporating domain knowledge and heuristics. Broadly, this paper demonstrates the effectiveness of tabled logic programming for planning, and argues the importance of modeling despite recent significant progress in domain-independent PDDL planners.

Dynamic Global Constraints: A First View

Global constraints proved themselves to be an efficient tool for modelling and solving large-scale real-life combinatorial problems. They encapsulate a set of binary constraints and using global reasoning about this set they filter the domains of involved variables better than arc consistency among the set of binary constraints. Moreover, global constraints exploit semantic information to achieve more efficient filtering than generalised consistency algorithms for n-ary constraints. Continued expansion of constraint programming (CP) to various application areas brings new challenges for design of global constraints. In particular, application of CP to advanced planning and scheduling (APS) requires dynamic additions of new variables and constraints during the process of constraint satisfaction and, thus, it would be helpful if the global constraints could adopt new variables. In the paper, we give a motivation for such dynamic global constraints and we describe a dynamic version of the well-known alldifferent constraint.

Interactive Timetabling

Timetabling is a typical application of constraint programming whose task is to allocate activities to slots in available resources respecting various constraints like precedence and capacity. In this paper we present a basic concept, a constraint model, and the solving algorithms for interactive timetabling. Interactive timetabling combines automated timetabling (the machine allocates the activities) with user interaction (the user can interfere with the process of timetabling). Because the user can see how the timetabling proceeds and can intervene this process, we believe that such approach is more convenient than full automated timetabling which behaves like a black-box. The contribution of this paper is twofold: we present a generic model to describe timetabling (and scheduling in general) problems and we propose an interactive algorithm for solving such problems.