Toward a Dynamic Programming Solution for the 4-peg Tower of Hanoi Problem with Configurations
Paper and Code
Jan 31, 2013
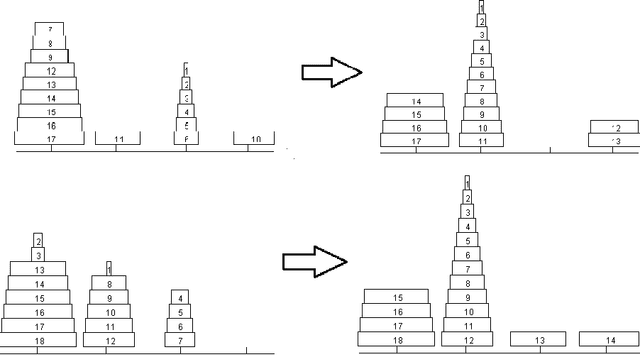
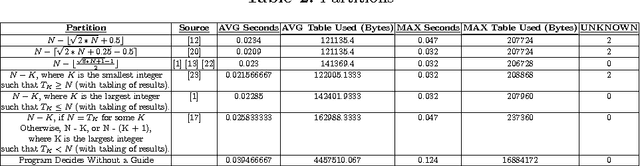

The Frame-Stewart algorithm for the 4-peg variant of the Tower of Hanoi, introduced in 1941, partitions disks into intermediate towers before moving the remaining disks to their destination. Algorithms that partition the disks have not been proven to be optimal, although they have been verified for up to 30 disks. This paper presents a dynamic programming approach to this algorithm, using tabling in B-Prolog. This study uses a variation of the problem, involving configurations of disks, in order to contrast the tabling approach with the approaches utilized by other solvers. A comparison of different partitioning locations for the Frame-Stewart algorithm indicates that, although certain partitions are optimal for the classic problem, they need to be modified for certain configurations, and that random configurations might require an entirely new algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge