Efficient Tabling Mechanisms for Transaction Logic Programs

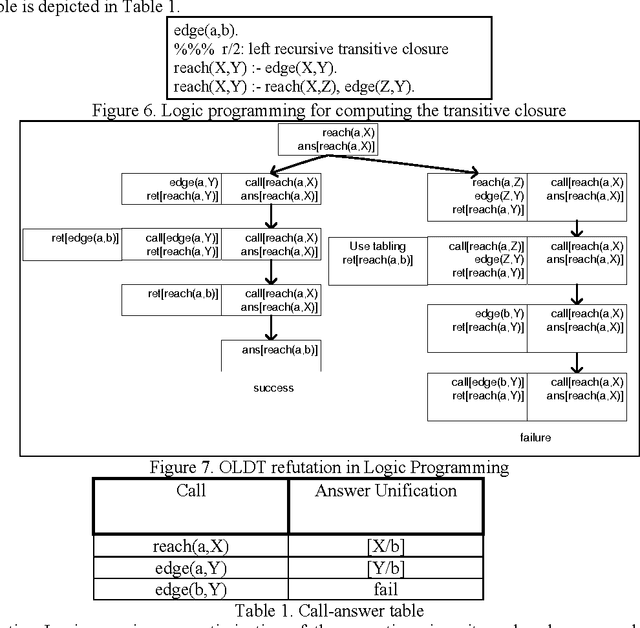
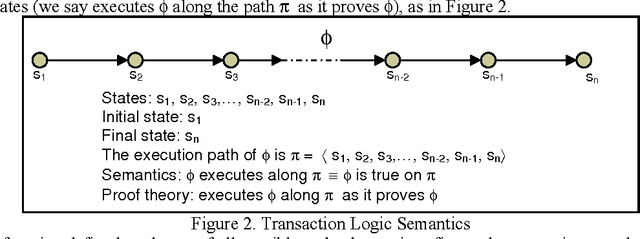
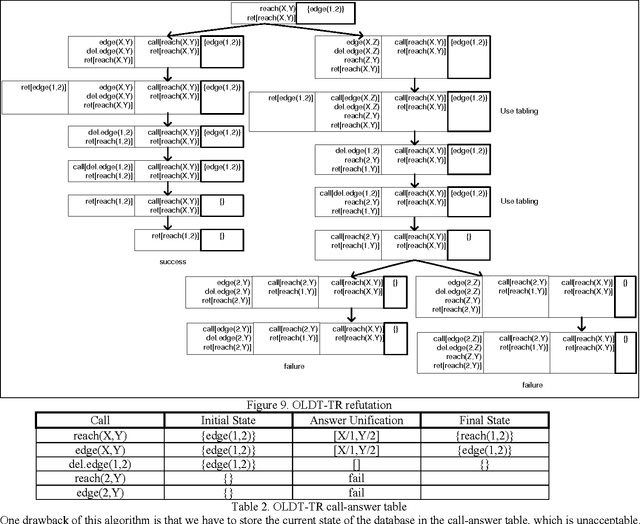
In this paper we present efficient evaluation algorithms for the Horn Transaction Logic (a generalization of the regular Horn logic programs with state updates). We present two complementary methods for optimizing the implementation of Transaction Logic. The first method is based on tabling and we modified the proof theory to table calls and answers on states (practically, equivalent to dynamic programming). The call-answer table is indexed on the call and a signature of the state in which the call was made. The answer columns contain the answer unification and a signature of the state after the call was executed. The states are signed efficiently using a technique based on tries and counting. The second method is based on incremental evaluation and it applies when the data oracle contains derived relations. The deletions and insertions (executed in the transaction oracle) change the state of the database. Using the heuristic of inertia (only a part of the state changes in response to elementary updates), most of the time it is cheaper to compute only the changes in the state than to recompute the entire state from scratch. The two methods are complementary by the fact that the first method optimizes the evaluation when a call is repeated in the same state, and the second method optimizes the evaluation of a new state when a call-state pair is not found by the tabling mechanism (i.e. the first method). The proof theory of Transaction Logic with the application of tabling and incremental evaluation is sound and complete with respect to its model theory.