Differentiable Inductive Logic Programming in High-Dimensional Space

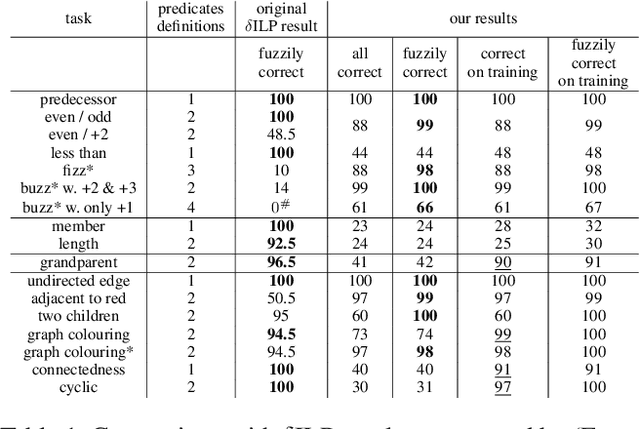
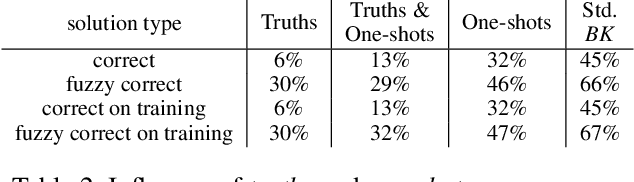
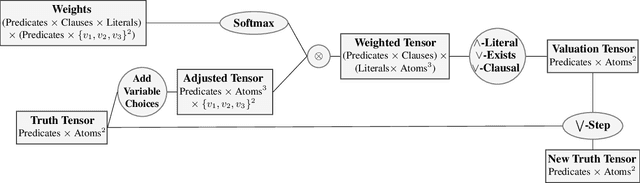
Synthesizing large logic programs through Inductive Logic Programming (ILP) typically requires intermediate definitions. However, cluttering the hypothesis space with intensional predicates often degrades performance. In contrast, gradient descent provides an efficient way to find solutions within such high-dimensional spaces. Neuro-symbolic ILP approaches have not fully exploited this so far. We propose an approach to ILP-based synthesis benefiting from large-scale predicate invention exploiting the efficacy of high-dimensional gradient descent. We find symbolic solutions containing upwards of ten auxiliary definitions. This is beyond the achievements of existing neuro-symbolic ILP systems, thus constituting a milestone in the field.

Adversarial Learning to Reason in an Arbitrary Logic

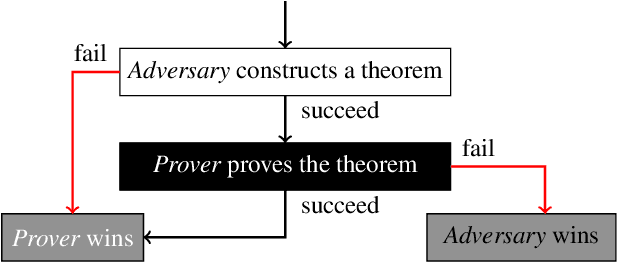
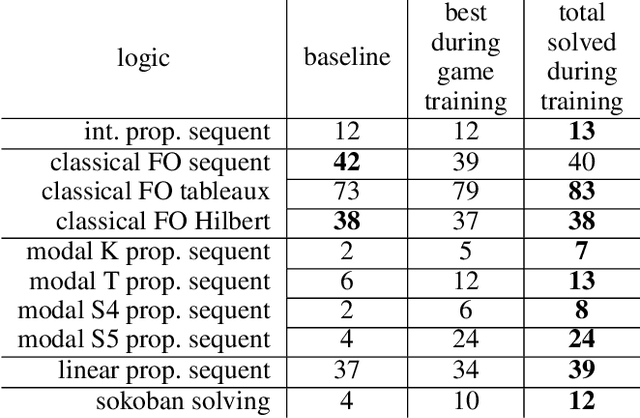
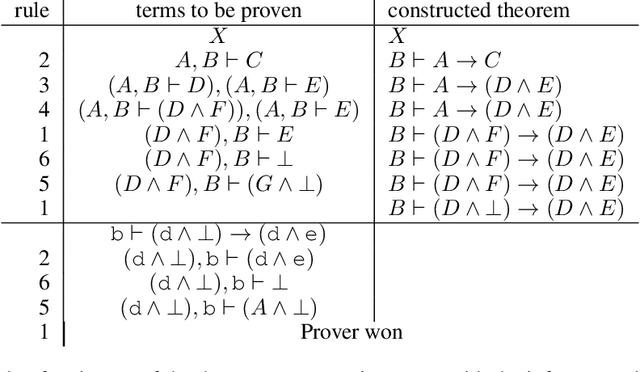
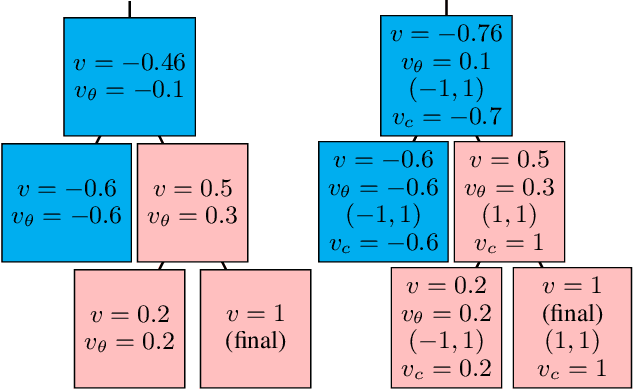
Existing approaches to learning to prove theorems focus on particular logics and datasets. In this work, we propose Monte-Carlo simulations guided by reinforcement learning that can work in an arbitrarily specified logic, without any human knowledge or set of problems. Since the algorithm does not need any training dataset, it is able to learn to work with any logical foundation, even when there is no body of proofs or even conjectures available. We practically demonstrate the feasibility of the approach in multiple logical systems. The approach is stronger than training on randomly generated data but weaker than the approaches trained on tailored axiom and conjecture sets. It however allows us to apply machine learning to automated theorem proving for many logics, where no such attempts have been tried to date, such as intuitionistic logic or linear logic.

Learning Higher-Order Programs without Meta-Interpretive Learning

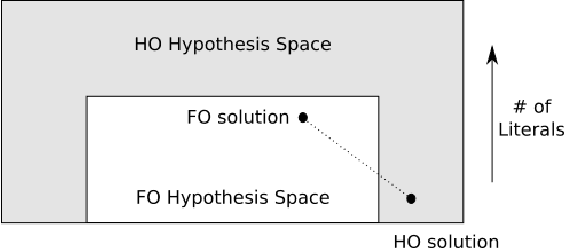
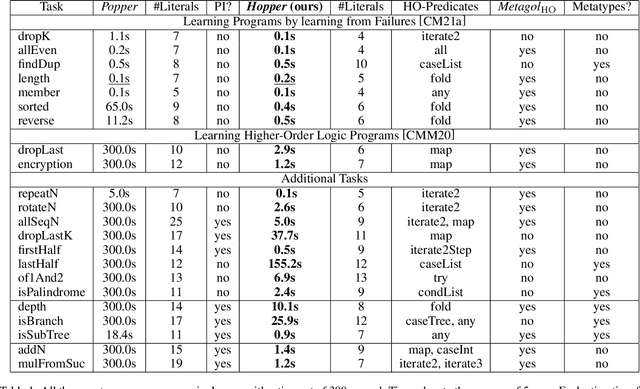
Learning complex programs through inductive logic programming (ILP) remains a formidable challenge. Existing higher-order enabled ILP systems show improved accuracy and learning performance, though remain hampered by the limitations of the underlying learning mechanism. Experimental results show that our extension of the versatile Learning From Failures paradigm by higher-order definitions significantly improves learning performance without the burdensome human guidance required by existing systems. Our theoretical framework captures a class of higher-order definitions preserving soundness of existing subsumption-based pruning methods.