Learning Sparse Causal Models is not NP-hard
Paper and Code
Sep 26, 2013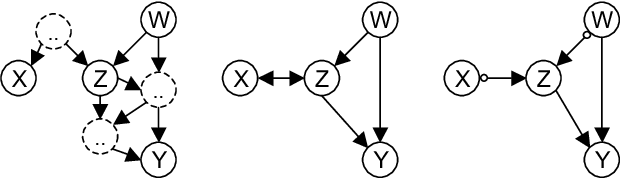
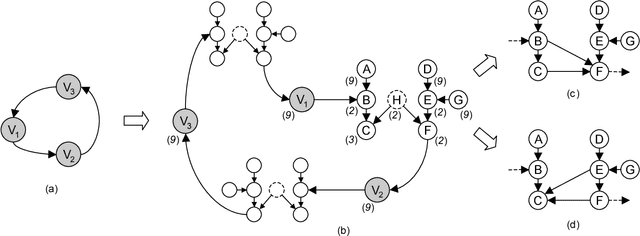
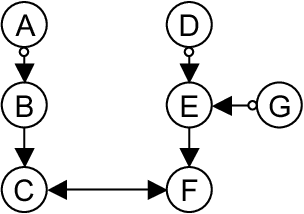
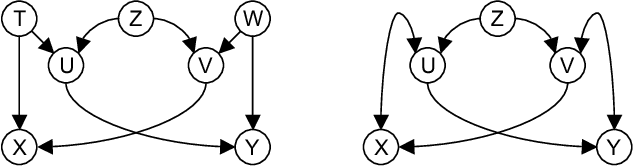
This paper shows that causal model discovery is not an NP-hard problem, in the sense that for sparse graphs bounded by node degree k the sound and complete causal model can be obtained in worst case order N^{2(k+2)} independence tests, even when latent variables and selection bias may be present. We present a modification of the well-known FCI algorithm that implements the method for an independence oracle, and suggest improvements for sample/real-world data versions. It does not contradict any known hardness results, and does not solve an NP-hard problem: it just proves that sparse causal discovery is perhaps more complicated, but not as hard as learning minimal Bayesian networks.
* Appears in Proceedings of the Twenty-Ninth Conference on Uncertainty
in Artificial Intelligence (UAI2013)
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge