Nonparametric Bayesian networks are typically faithful in the total variation metric

We show that for a given DAG $G$, among all observational distributions of Bayesian networks over $G$ with arbitrary outcome spaces, the faithful distributions are `typical': they constitute a dense, open set with respect to the total variation metric. As a consequence, the set of faithful distributions is non-empty, and the unfaithful distributions are nowhere dense. We extend this result to the space of Bayesian networks, where the properties hold for Bayesian networks instead of distributions of Bayesian networks. As special cases, we show that these results also hold for the faithful parameters of the subclasses of linear Gaussian -- and discrete Bayesian networks, giving a topological analogue of the measure-zero results of Spirtes et al. (1993) and Meek (1995). Finally, we extend our topological results and the measure-zero results of Spirtes et al. and Meek to Bayesian networks with latent variables.

Dynamic Structural Causal Models

We study a specific type of SCM, called a Dynamic Structural Causal Model (DSCM), whose endogenous variables represent functions of time, which is possibly cyclic and allows for latent confounding. As a motivating use-case, we show that certain systems of Stochastic Differential Equations (SDEs) can be appropriately represented with DSCMs. An immediate consequence of this construction is a graphical Markov property for systems of SDEs. We define a time-splitting operation, allowing us to analyse the concept of local independence (a notion of continuous-time Granger (non-)causality). We also define a subsampling operation, which returns a discrete-time DSCM, and which can be used for mathematical analysis of subsampled time-series. We give suggestions how DSCMs can be used for identification of the causal effect of time-dependent interventions, and how existing constraint-based causal discovery algorithms can be applied to time-series data.

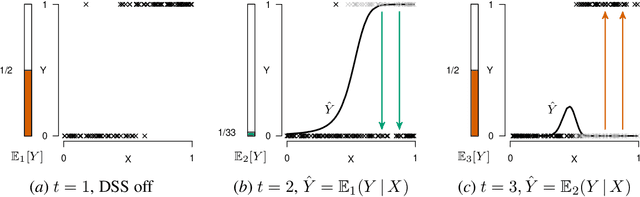
Evaluating and Correcting Performative Effects of Decision Support Systems via Causal Domain Shift

When predicting a target variable $Y$ from features $X$, the prediction $\hat{Y}$ can be performative: an agent might act on this prediction, affecting the value of $Y$ that we eventually observe. Performative predictions are deliberately prevalent in algorithmic decision support, where a Decision Support System (DSS) provides a prediction for an agent to affect the value of the target variable. When deploying a DSS in high-stakes settings (e.g. healthcare, law, predictive policing, or child welfare screening) it is imperative to carefully assess the performative effects of the DSS. In the case that the DSS serves as an alarm for a predicted negative outcome, naive retraining of the prediction model is bound to result in a model that underestimates the risk, due to effective workings of the previous model. In this work, we propose to model the deployment of a DSS as causal domain shift and provide novel cross-domain identification results for the conditional expectation $E[Y | X]$, allowing for pre- and post-hoc assessment of the deployment of the DSS, and for retraining of a model that assesses the risk under a baseline policy where the DSS is not deployed. Using a running example, we empirically show that a repeated regression procedure provides a practical framework for estimating these quantities, even when the data is affected by sample selection bias and selective labelling, offering for a practical, unified solution for multiple forms of target variable bias.

Correcting for Selection Bias and Missing Response in Regression using Privileged Information

When estimating a regression model, we might have data where some labels are missing, or our data might be biased by a selection mechanism. When the response or selection mechanism is ignorable (i.e., independent of the response variable given the features) one can use off-the-shelf regression methods; in the nonignorable case one typically has to adjust for bias. We observe that privileged data (i.e. data that is only available during training) might render a nonignorable selection mechanism ignorable, and we refer to this scenario as Privilegedly Missing at Random (PMAR). We propose a novel imputation-based regression method, named repeated regression, that is suitable for PMAR. We also consider an importance weighted regression method, and a doubly robust combination of the two. The proposed methods are easy to implement with most popular out-of-the-box regression algorithms. We empirically assess the performance of the proposed methods with extensive simulated experiments and on a synthetically augmented real-world dataset. We conclude that repeated regression can appropriately correct for bias, and can have considerable advantage over weighted regression, especially when extrapolating to regions of the feature space where response is never observed.