ModShift: Model Privacy via Designed Shifts

In this paper, shifts are introduced to preserve model privacy against an eavesdropper in federated learning. Model learning is treated as a parameter estimation problem. This perspective allows us to derive the Fisher Information matrix of the model updates from the shifted updates and drive them to singularity, thus posing a hard estimation problem for Eve. The shifts are securely shared with the central server to maintain model accuracy at the server and participating devices. A convergence test is proposed to detect if model updates have been tampered with and we show that our scheme passes this test. Numerical results show that our scheme achieves a higher model shift when compared to a noise injection scheme while requiring a lesser bandwidth secret channel.

Delay-Angle Information Spoofing for Channel State Information-Free Location-Privacy Enhancement

In this paper, a delay-angle information spoofing (DAIS) strategy is proposed to enhance the location privacy at the physical layer. More precisely, the location-relevant delays and angles are artificially shifted without the aid of channel state information (CSI) at the transmitter, such that the location perceived by the eavesdropper is incorrect and distinct from the true one. By leveraging the intrinsic structure of the wireless channel, a precoder is designed to achieve DAIS while the legitimate localizer can remove the obfuscation via securely receiving a modest amount of information, i.e., the delay-angle shifts. A lower bound on eavesdropper's localization error is derived, revealing that location privacy is enhanced not only due to estimation error, but also by the geometric mismatch introduced by DAIS. Furthermore, the lower bound is explicitly expressed as a function of the delay-angle shifts, characterizing performance trends and providing the appropriate design of these shift parameters. The statistical hardness of maliciously inferring the delay-angle shifts by a single-antenna eavesdropper as well as the challenges for a multi-antenna eavesdropper are investigated to assess the robustness of the proposed DAIS strategy. Numerical results show that the proposed DAIS strategy results in more than 15 dB performance degradation for the eavesdropper as compared with that for the legitimate localizer at high signal-to-noise ratios, and provides more effective location-privacy enhancement than the prior art.

Generative Multi-Agent Q-Learning for Policy Optimization: Decentralized Wireless Networks

Q-learning is a widely used reinforcement learning (RL) algorithm for optimizing wireless networks, but faces challenges with large state-spaces. Recently proposed multi-environment mixed Q-learning (MEMQ) algorithm addresses these challenges by employing multiple Q-learning algorithms across multiple synthetically generated, distinct but structurally related environments, so-called digital cousins. In this paper, we propose a novel multi-agent MEMQ (M-MEMQ) for cooperative decentralized wireless networks with multiple networked transmitters (TXs) and base stations (BSs). TXs do not have access to global information (joint state and actions). The new concept of coordinated and uncoordinated states is introduced. In uncoordinated states, TXs act independently to minimize their individual costs and update local Q-functions. In coordinated states, TXs use a Bayesian approach to estimate the joint state and update the joint Q-functions. The cost of information-sharing scales linearly with the number of TXs and is independent of the joint state-action space size. Several theoretical guarantees, including deterministic and probabilistic convergence, bounds on estimation error variance, and the probability of misdetecting the joint states, are given. Numerical simulations show that M-MEMQ outperforms several decentralized and centralized training with decentralized execution (CTDE) multi-agent RL algorithms by achieving 55% lower average policy error (APE), 35% faster convergence, 50% reduced runtime complexity, and 45% less sample complexity. Furthermore, M-MEMQ achieves comparable APE with significantly lower complexity than centralized methods. Simulations validate the theoretical analyses.

Coverage Analysis for Digital Cousin Selection -- Improving Multi-Environment Q-Learning

Q-learning is widely employed for optimizing various large-dimensional networks with unknown system dynamics. Recent advancements include multi-environment mixed Q-learning (MEMQ) algorithms, which utilize multiple independent Q-learning algorithms across multiple, structurally related but distinct environments and outperform several state-of-the-art Q-learning algorithms in terms of accuracy, complexity, and robustness. We herein conduct a comprehensive probabilistic coverage analysis to ensure optimal data coverage conditions for MEMQ algorithms. First, we derive upper and lower bounds on the expectation and variance of different coverage coefficients (CC) for MEMQ algorithms. Leveraging these bounds, we develop a simple way of comparing the utilities of multiple environments in MEMQ algorithms. This approach appears to be near optimal versus our previously proposed partial ordering approach. We also present a novel CC-based MEMQ algorithm to improve the accuracy and complexity of existing MEMQ algorithms. Numerical experiments are conducted using random network graphs with four different graph properties. Our algorithm can reduce the average policy error (APE) by 65% compared to partial ordering and is 95% faster than the exhaustive search. It also achieves 60% less APE than several state-of-the-art reinforcement learning and prior MEMQ algorithms. Additionally, we numerically verify the theoretical results and show their scalability with the action-space size.

A Multi-Agent Multi-Environment Mixed Q-Learning for Partially Decentralized Wireless Network Optimization

Q-learning is a powerful tool for network control and policy optimization in wireless networks, but it struggles with large state spaces. Recent advancements, like multi-environment mixed Q-learning (MEMQ), improves performance and reduces complexity by integrating multiple Q-learning algorithms across multiple related environments so-called digital cousins. However, MEMQ is designed for centralized single-agent networks and is not suitable for decentralized or multi-agent networks. To address this challenge, we propose a novel multi-agent MEMQ algorithm for partially decentralized wireless networks with multiple mobile transmitters (TXs) and base stations (BSs), where TXs do not have access to each other's states and actions. In uncoordinated states, TXs act independently to minimize their individual costs. In coordinated states, TXs use a Bayesian approach to estimate the joint state based on local observations and share limited information with leader TX to minimize joint cost. The cost of information sharing scales linearly with the number of TXs and is independent of the joint state-action space size. The proposed scheme is 50% faster than centralized MEMQ with only a 20% increase in average policy error (APE) and is 25% faster than several advanced decentralized Q-learning algorithms with 40% less APE. The convergence of the algorithm is also demonstrated.

Coverage Analysis of Multi-Environment Q-Learning Algorithms for Wireless Network Optimization

Q-learning is widely used to optimize wireless networks with unknown system dynamics. Recent advancements include ensemble multi-environment hybrid Q-learning algorithms, which utilize multiple Q-learning algorithms across structurally related but distinct Markovian environments and outperform existing Q-learning algorithms in terms of accuracy and complexity in large-scale wireless networks. We herein conduct a comprehensive coverage analysis to ensure optimal data coverage conditions for these algorithms. Initially, we establish upper bounds on the expectation and variance of different coverage coefficients. Leveraging these bounds, we present an algorithm for efficient initialization of these algorithms. We test our algorithm on two distinct real-world wireless networks. Numerical simulations show that our algorithm can achieve %50 less policy error and %40 less runtime complexity than state-of-the-art reinforcement learning algorithms. Furthermore, our algorithm exhibits robustness to changes in network settings and parameters. We also numerically validate our theoretical results.

Asymmetric Graph Error Control with Low Complexity in Causal Bandits

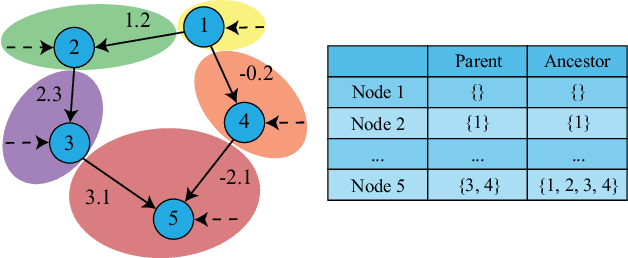
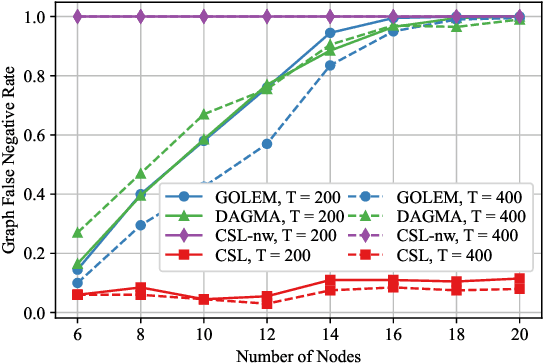
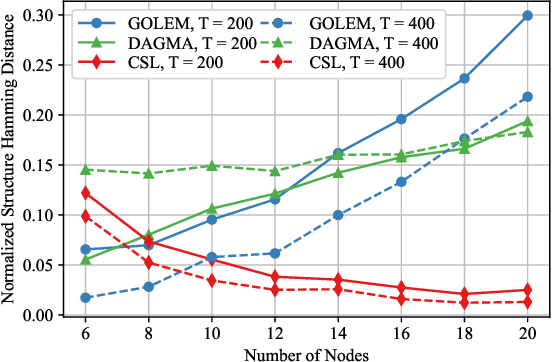
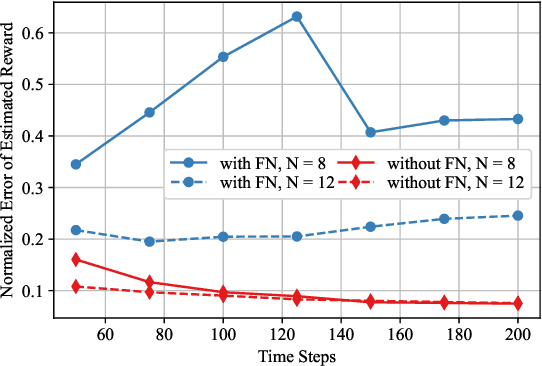
In this paper, the causal bandit problem is investigated, in which the objective is to select an optimal sequence of interventions on nodes in a causal graph. It is assumed that the graph is governed by linear structural equations; it is further assumed that both the causal topology and the distribution of interventions are unknown. By exploiting the causal relationships between the nodes whose signals contribute to the reward, interventions are optimized. First, based on the difference between the two types of graph identification errors (false positives and negatives), a causal graph learning method is proposed, which strongly reduces sample complexity relative to the prior art by learning sub-graphs. Under the assumption of Gaussian exogenous inputs and minimum-mean squared error weight estimation, a new uncertainty bound tailored to the causal bandit problem is derived. This uncertainty bound drives an upper confidence bound based intervention selection to optimize the reward. To cope with non-stationary bandits, a sub-graph change detection mechanism is proposed, with high sample efficiency. Numerical results compare the new methodology to existing schemes and show a substantial performance improvement in both stationary and non-stationary settings. Compared to existing approaches, the proposed scheme takes 67% fewer samples to learn the causal structure and achieves an average reward gain of 85%.

Can FSK Be Optimised for Integrated Sensing and Communications?

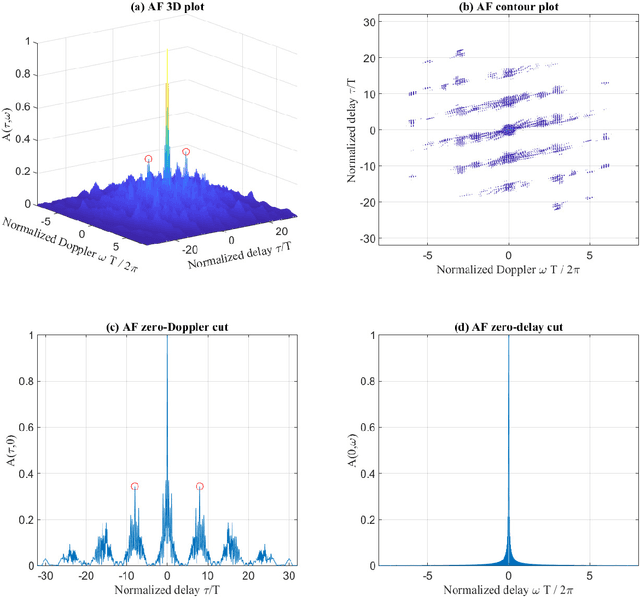
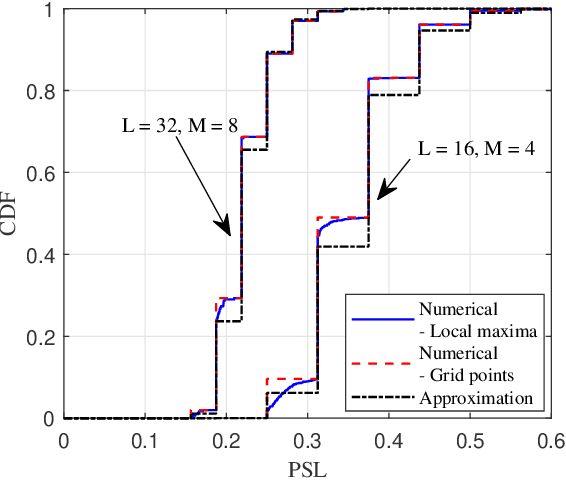
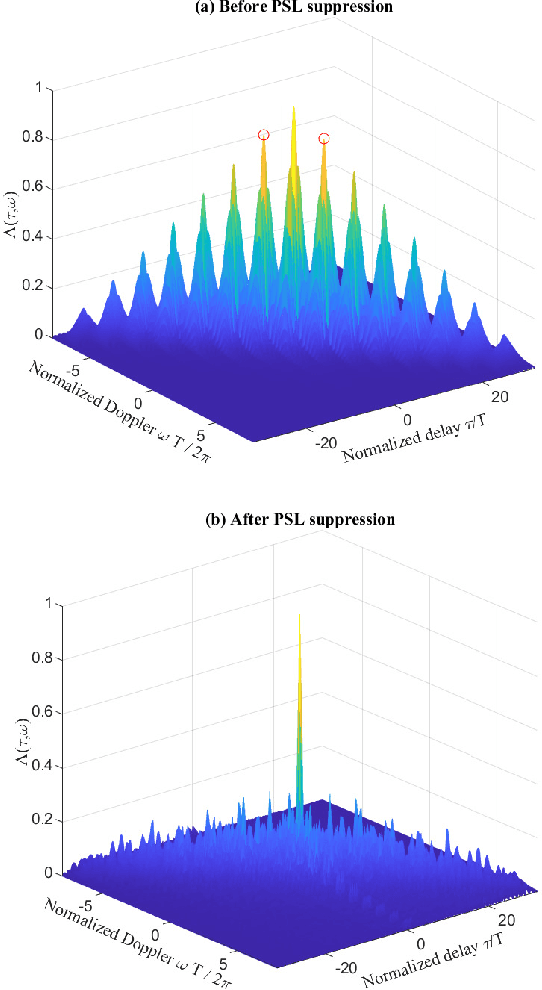
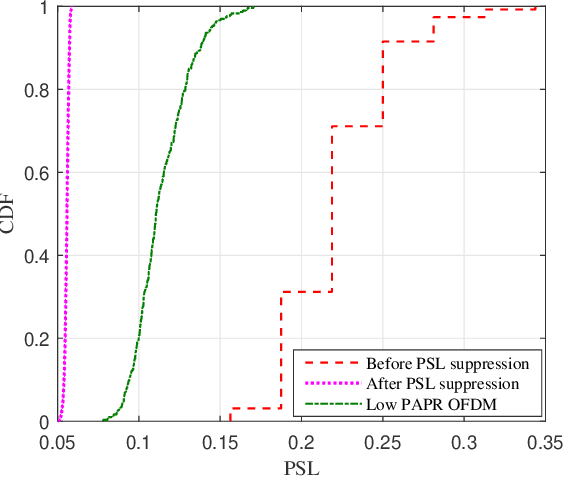
Motivated by the ideal peak-to-average-power ratio and radar sensing capability of traditional frequency-coded radar waveforms, this paper considers the frequency shift keying (FSK) based waveform for joint communications and radar (JCR). An analysis of the probability distributions of its ambiguity function (AF) sidelobe levels (SLs) and peak sidelobe level (PSL) is conducted to study the radar sensing capability of random FSK. Numerical results show that the independent frequency modulation introduces uncontrollable AF PSLs. In order to address this problem, the initial phases of waveform sub-pulses are designed by solving a min-max optimisation problem. Numerical results indicate that the optimisation-based phase design can effectively reduce the AF PSL to a level close to well-designed radar waveforms while having no impact on the data rate and the receiver complexity. For large numbers of waveform sub-pulses and modulation orders, the impact on the error probability is also insignificant.

Leveraging Digital Cousins for Ensemble Q-Learning in Large-Scale Wireless Networks

Optimizing large-scale wireless networks, including optimal resource management, power allocation, and throughput maximization, is inherently challenging due to their non-observable system dynamics and heterogeneous and complex nature. Herein, a novel ensemble Q-learning algorithm that addresses the performance and complexity challenges of the traditional Q-learning algorithm for optimizing wireless networks is presented. Ensemble learning with synthetic Markov Decision Processes is tailored to wireless networks via new models for approximating large state-space observable wireless networks. In particular, digital cousins are proposed as an extension of the traditional digital twin concept wherein multiple Q-learning algorithms on multiple synthetic Markovian environments are run in parallel and their outputs are fused into a single Q-function. Convergence analyses of key statistics and Q-functions and derivations of upper bounds on the estimation bias and variance are provided. Numerical results across a variety of real-world wireless networks show that the proposed algorithm can achieve up to 50% less average policy error with up to 40% less runtime complexity than the state-of-the-art reinforcement learning algorithms. It is also shown that theoretical results properly predict trends in the experimental results.

Multi-Timescale Ensemble Q-learning for Markov Decision Process Policy Optimization

Reinforcement learning (RL) is a classical tool to solve network control or policy optimization problems in unknown environments. The original Q-learning suffers from performance and complexity challenges across very large networks. Herein, a novel model-free ensemble reinforcement learning algorithm which adapts the classical Q-learning is proposed to handle these challenges for networks which admit Markov decision process (MDP) models. Multiple Q-learning algorithms are run on multiple, distinct, synthetically created and structurally related Markovian environments in parallel; the outputs are fused using an adaptive weighting mechanism based on the Jensen-Shannon divergence (JSD) to obtain an approximately optimal policy with low complexity. The theoretical justification of the algorithm, including the convergence of key statistics and Q-functions are provided. Numerical results across several network models show that the proposed algorithm can achieve up to 55% less average policy error with up to 50% less runtime complexity than the state-of-the-art Q-learning algorithms. Numerical results validate assumptions made in the theoretical analysis.