Can Cross-Layer Transcoders Replace Vision Transformer Activations? An Interpretable Perspective on Vision

Understanding the internal activations of Vision Transformers (ViTs) is critical for building interpretable and trustworthy models. While Sparse Autoencoders (SAEs) have been used to extract human-interpretable features, they operate on individual layers and fail to capture the cross-layer computational structure of Transformers, as well as the relative significance of each layer in forming the last-layer representation. Alternatively, we introduce the adoption of Cross-Layer Transcoders (CLTs) as reliable, sparse, and depth-aware proxy models for MLP blocks in ViTs. CLTs use an encoder-decoder scheme to reconstruct each post-MLP activation from learned sparse embeddings of preceding layers, yielding a linear decomposition that transforms the final representation of ViTs from an opaque embedding into an additive, layer-resolved construction that enables faithful attribution and process-level interpretability. We train CLTs on CLIP ViT-B/32 and ViT-B/16 across CIFAR-100, COCO, and ImageNet-100. We show that CLTs achieve high reconstruction fidelity with post-MLP activations while preserving and even improving, in some cases, CLIP zero-shot classification accuracy. In terms of interpretability, we show that the cross-layer contribution scores provide faithful attribution, revealing that the final representation is concentrated in a smaller set of dominant layer-wise terms whose removal degrades performance and whose retention largely preserves it. These results showcase the significance of adopting CLTs as an alternative interpretable proxy of ViTs in the vision domain.

3D Scene Rendering with Multimodal Gaussian Splatting

3D scene reconstruction and rendering are core tasks in computer vision, with applications spanning industrial monitoring, robotics, and autonomous driving. Recent advances in 3D Gaussian Splatting (GS) and its variants have achieved impressive rendering fidelity while maintaining high computational and memory efficiency. However, conventional vision-based GS pipelines typically rely on a sufficient number of camera views to initialize the Gaussian primitives and train their parameters, typically incurring additional processing cost during initialization while falling short in conditions where visual cues are unreliable, such as adverse weather, low illumination, or partial occlusions. To cope with these challenges, and motivated by the robustness of radio-frequency (RF) signals to weather, lighting, and occlusions, we introduce a multimodal framework that integrates RF sensing, such as automotive radar, with GS-based rendering as a more efficient and robust alternative to vision-only GS rendering. The proposed approach enables efficient depth prediction from only sparse RF-based depth measurements, yielding a high-quality 3D point cloud for initializing Gaussian functions across diverse GS architectures. Numerical tests demonstrate the merits of judiciously incorporating RF sensing into GS pipelines, achieving high-fidelity 3D scene rendering driven by RF-informed structural accuracy.

ActiveInitSplat: How Active Image Selection Helps Gaussian Splatting

Gaussian splatting (GS) along with its extensions and variants provides outstanding performance in real-time scene rendering while meeting reduced storage demands and computational efficiency. While the selection of 2D images capturing the scene of interest is crucial for the proper initialization and training of GS, hence markedly affecting the rendering performance, prior works rely on passively and typically densely selected 2D images. In contrast, this paper proposes `ActiveInitSplat', a novel framework for active selection of training images for proper initialization and training of GS. ActiveInitSplat relies on density and occupancy criteria of the resultant 3D scene representation from the selected 2D images, to ensure that the latter are captured from diverse viewpoints leading to better scene coverage and that the initialized Gaussian functions are well aligned with the actual 3D structure. Numerical tests on well-known simulated and real environments demonstrate the merits of ActiveInitSplat resulting in significant GS rendering performance improvement over passive GS baselines, in the widely adopted LPIPS, SSIM, and PSNR metrics.

3D Reconstruction in Noisy Agricultural Environments: A Bayesian Optimization Perspective for View Planning

3D reconstruction is a fundamental task in robotics that gained attention due to its major impact in a wide variety of practical settings, including agriculture, underwater, and urban environments. An important approach for this task, known as view planning, is to judiciously place a number of cameras in positions that maximize the visual information improving the resulting 3D reconstruction. Circumventing the need for a large number of arbitrary images, geometric criteria can be applied to select fewer yet more informative images to markedly improve the 3D reconstruction performance. Nonetheless, incorporating the noise of the environment that exists in various real-world scenarios into these criteria may be challenging, particularly when prior information about the noise is not provided. To that end, this work advocates a novel geometric function that accounts for the existing noise, relying solely on a relatively small number of noise realizations without requiring its closed-form expression. With no analytic expression of the geometric function, this work puts forth a Bayesian optimization algorithm for accurate 3D reconstruction in the presence of noise. Numerical tests on noisy agricultural environments showcase the impressive merits of the proposed approach for 3D reconstruction with even a small number of available cameras.

Weighted Ensembles for Active Learning with Adaptivity

Labeled data can be expensive to acquire in several application domains, including medical imaging, robotics, and computer vision. To efficiently train machine learning models under such high labeling costs, active learning (AL) judiciously selects the most informative data instances to label on-the-fly. This active sampling process can benefit from a statistical function model, that is typically captured by a Gaussian process (GP). While most GP-based AL approaches rely on a single kernel function, the present contribution advocates an ensemble of GP models with weights adapted to the labeled data collected incrementally. Building on this novel EGP model, a suite of acquisition functions emerges based on the uncertainty and disagreement rules. An adaptively weighted ensemble of EGP-based acquisition functions is also introduced to further robustify performance. Extensive tests on synthetic and real datasets showcase the merits of the proposed EGP-based approaches with respect to the single GP-based AL alternatives.

Surrogate modeling for Bayesian optimization beyond a single Gaussian process

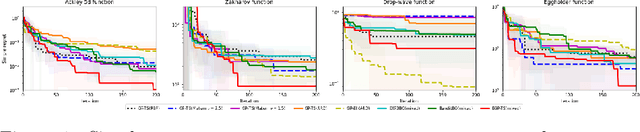
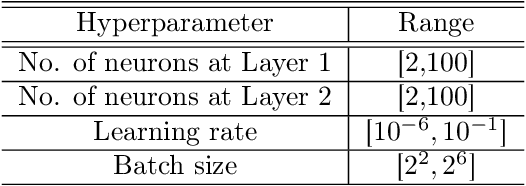
Bayesian optimization (BO) has well-documented merits for optimizing black-box functions with an expensive evaluation cost. Such functions emerge in applications as diverse as hyperparameter tuning, drug discovery, and robotics. BO hinges on a Bayesian surrogate model to sequentially select query points so as to balance exploration with exploitation of the search space. Most existing works rely on a single Gaussian process (GP) based surrogate model, where the kernel function form is typically preselected using domain knowledge. To bypass such a design process, this paper leverages an ensemble (E) of GPs to adaptively select the surrogate model fit on-the-fly, yielding a GP mixture posterior with enhanced expressiveness for the sought function. Acquisition of the next evaluation input using this EGP-based function posterior is then enabled by Thompson sampling (TS) that requires no additional design parameters. To endow function sampling with scalability, random feature-based kernel approximation is leveraged per GP model. The novel EGP-TS readily accommodates parallel operation. To further establish convergence of the proposed EGP-TS to the global optimum, analysis is conducted based on the notion of Bayesian regret for both sequential and parallel settings. Tests on synthetic functions and real-world applications showcase the merits of the proposed method.

Unveiling Anomalous Edges and Nominal Connectivity of Attributed Networks

Uncovering anomalies in attributed networks has recently gained popularity due to its importance in unveiling outliers and flagging adversarial behavior in a gamut of data and network science applications including {the Internet of Things (IoT)}, finance, security, to list a few. The present work deals with uncovering anomalous edges in attributed graphs using two distinct formulations with complementary strengths, which can be easily distributed, and hence efficient. The first relies on decomposing the graph data matrix into low rank plus sparse components to markedly improve performance. The second broadens the scope of the first by performing robust recovery of the unperturbed graph, which enhances the anomaly identification performance. The novel methods not only capture anomalous edges linking nodes of different communities, but also spurious connections between any two nodes with different features. Experiments conducted on real and synthetic data corroborate the effectiveness of both methods in the anomaly identification task.