Principal Manifold Flows
Paper and Code
Feb 14, 2022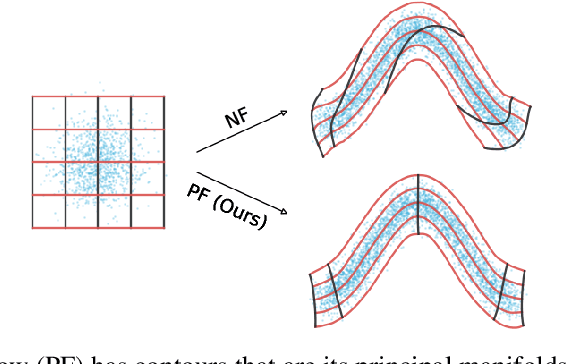

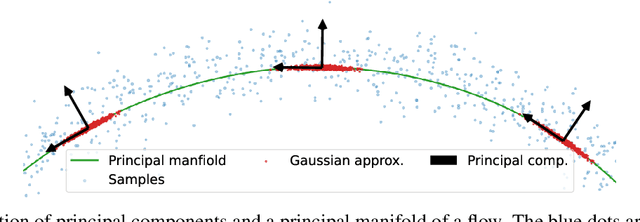

Normalizing flows map an independent set of latent variables to their samples using a bijective transformation. Despite the exact correspondence between samples and latent variables, their high level relationship is not well understood. In this paper we characterize the geometric structure of flows using principal manifolds and understand the relationship between latent variables and samples using contours. We introduce a novel class of normalizing flows, called principal manifold flows (PF), whose contours are its principal manifolds, and a variant for injective flows (iPF) that is more efficient to train than regular injective flows. PFs can be constructed using any flow architecture, are trained with a regularized maximum likelihood objective and can perform density estimation on all of their principal manifolds. In our experiments we show that PFs and iPFs are able to learn the principal manifolds over a variety of datasets. Additionally, we show that PFs can perform density estimation on data that lie on a manifold with variable dimensionality, which is not possible with existing normalizing flows.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge