Gerome Miklau
Joint Selection: Adaptively Incorporating Public Information for Private Synthetic Data
Mar 12, 2024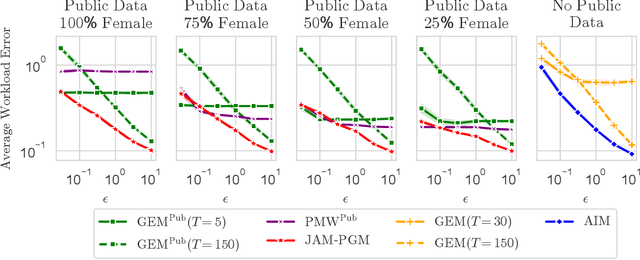
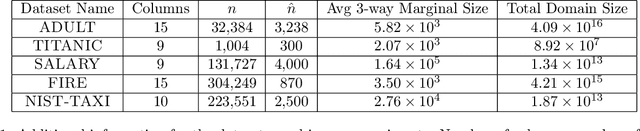
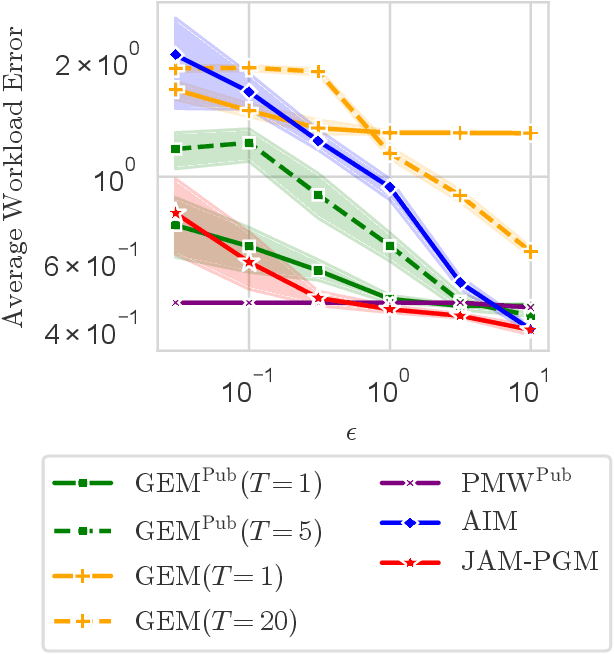
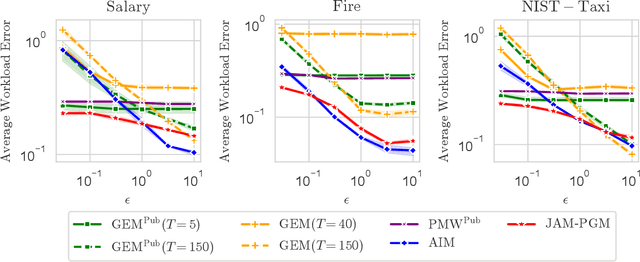
Abstract:Mechanisms for generating differentially private synthetic data based on marginals and graphical models have been successful in a wide range of settings. However, one limitation of these methods is their inability to incorporate public data. Initializing a data generating model by pre-training on public data has shown to improve the quality of synthetic data, but this technique is not applicable when model structure is not determined a priori. We develop the mechanism jam-pgm, which expands the adaptive measurements framework to jointly select between measuring public data and private data. This technique allows for public data to be included in a graphical-model-based mechanism. We show that jam-pgm is able to outperform both publicly assisted and non publicly assisted synthetic data generation mechanisms even when the public data distribution is biased.
Relaxed Marginal Consistency for Differentially Private Query Answering
Sep 13, 2021


Abstract:Many differentially private algorithms for answering database queries involve a step that reconstructs a discrete data distribution from noisy measurements. This provides consistent query answers and reduces error, but often requires space that grows exponentially with dimension. Private-PGM is a recent approach that uses graphical models to represent the data distribution, with complexity proportional to that of exact marginal inference in a graphical model with structure determined by the co-occurrence of variables in the noisy measurements. Private-PGM is highly scalable for sparse measurements, but may fail to run in high dimensions with dense measurements. We overcome the main scalability limitation of Private-PGM through a principled approach that relaxes consistency constraints in the estimation objective. Our new approach works with many existing private query answering algorithms and improves scalability or accuracy with no privacy cost.
Privacy Preserving Off-Policy Evaluation
Feb 01, 2019



Abstract:Many reinforcement learning applications involve the use of data that is sensitive, such as medical records of patients or financial information. However, most current reinforcement learning methods can leak information contained within the (possibly sensitive) data on which they are trained. To address this problem, we present the first differentially private approach for off-policy evaluation. We provide a theoretical analysis of the privacy-preserving properties of our algorithm and analyze its utility (speed of convergence). After describing some results of this theoretical analysis, we show empirically that our method outperforms previous methods (which are restricted to the on-policy setting).
Graphical-model based estimation and inference for differential privacy
Jan 26, 2019



Abstract:Many privacy mechanisms reveal high-level information about a data distribution through noisy measurements. It is common to use this information to estimate the answers to new queries. In this work, we provide an approach to solve this estimation problem efficiently using graphical models, which is particularly effective when the distribution is high-dimensional but the measurements are over low-dimensional marginals. We show that our approach is far more efficient than existing estimation techniques from the privacy literature and that it can improve the accuracy and scalability of many state-of-the-art mechanisms.
Differentially Private Learning of Undirected Graphical Models using Collective Graphical Models
Jun 14, 2017


Abstract:We investigate the problem of learning discrete, undirected graphical models in a differentially private way. We show that the approach of releasing noisy sufficient statistics using the Laplace mechanism achieves a good trade-off between privacy, utility, and practicality. A naive learning algorithm that uses the noisy sufficient statistics "as is" outperforms general-purpose differentially private learning algorithms. However, it has three limitations: it ignores knowledge about the data generating process, rests on uncertain theoretical foundations, and exhibits certain pathologies. We develop a more principled approach that applies the formalism of collective graphical models to perform inference over the true sufficient statistics within an expectation-maximization framework. We show that this learns better models than competing approaches on both synthetic data and on real human mobility data used as a case study.
Scalable Probabilistic Databases with Factor Graphs and MCMC
May 11, 2010



Abstract:Probabilistic databases play a crucial role in the management and understanding of uncertain data. However, incorporating probabilities into the semantics of incomplete databases has posed many challenges, forcing systems to sacrifice modeling power, scalability, or restrict the class of relational algebra formula under which they are closed. We propose an alternative approach where the underlying relational database always represents a single world, and an external factor graph encodes a distribution over possible worlds; Markov chain Monte Carlo (MCMC) inference is then used to recover this uncertainty to a desired level of fidelity. Our approach allows the efficient evaluation of arbitrary queries over probabilistic databases with arbitrary dependencies expressed by graphical models with structure that changes during inference. MCMC sampling provides efficiency by hypothesizing {\em modifications} to possible worlds rather than generating entire worlds from scratch. Queries are then run over the portions of the world that change, avoiding the onerous cost of running full queries over each sampled world. A significant innovation of this work is the connection between MCMC sampling and materialized view maintenance techniques: we find empirically that using view maintenance techniques is several orders of magnitude faster than naively querying each sampled world. We also demonstrate our system's ability to answer relational queries with aggregation, and demonstrate additional scalability through the use of parallelization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge