Unscented Gaussian Process Latent Variable Model: learning from uncertain inputs with intractable kernels

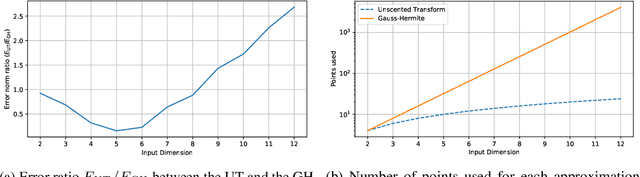
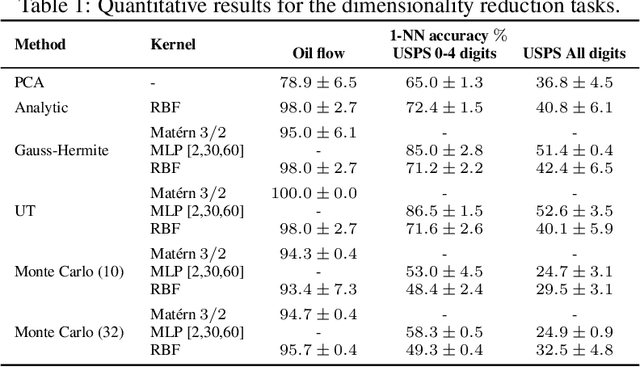
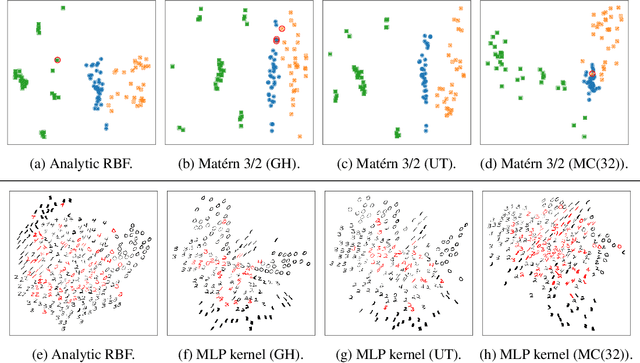
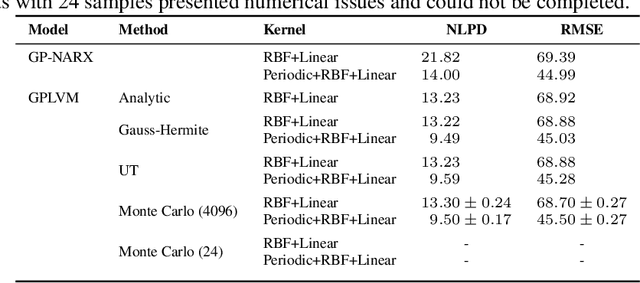
The Gaussian Process (GP) framework flexibility has enabled its use in several data modeling scenarios. The setting where we have unavailable or uncertain inputs that generate possibly noisy observations is usually tackled by the well known Gaussian Process Latent Variable Model (GPLVM). However, the standard variational approach to perform inference with the GPLVM presents some expressions that are tractable for only a few kernel functions, which may hinder its general application. While other quadrature or sampling approaches could be used in that case, they usually are very slow and/or non-deterministic. In the present paper, we propose the use of the unscented transformation to enable the use of any kernel function within the Bayesian GPLVM. Our approach maintains the fully deterministic feature of tractable kernels and presents a simple implementation with only moderate computational cost. Experiments on dimensionality reduction and multistep-ahead prediction with uncertainty propagation indicate the feasibility of our proposal.