Minimal Learning Machine: Theoretical Results and Clustering-Based Reference Point Selection
Paper and Code
Sep 22, 2019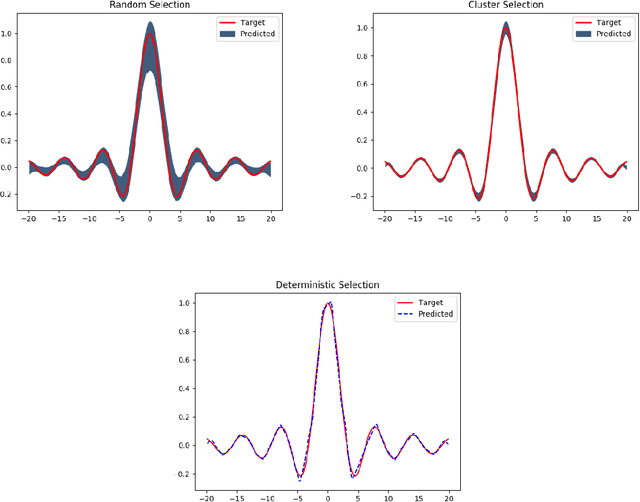

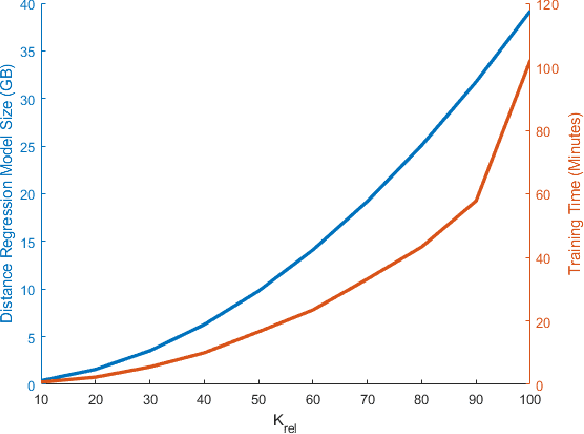
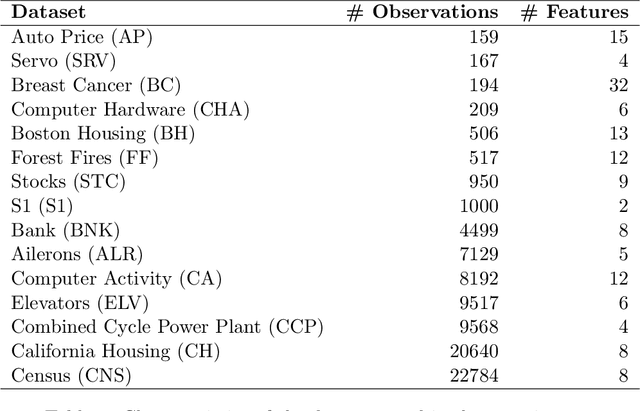
The Minimal Learning Machine (MLM) is a nonlinear supervised approach based on learning a linear mapping between distance matrices computed in the input and output data spaces, where distances are calculated concerning a subset of points called reference points. Its simple formulation has attracted several recent works on extensions and applications. In this paper, we aim to address some open questions related to the MLM. First, we detail theoretical aspects that assure the interpolation and universal approximation capabilities of the MLM, which were previously only empirically verified. Second, we identify the task of selecting reference points as having major importance for the MLM's generalization capability; furthermore, we assess several clustering-based methods in regression scenarios. Based on an extensive empirical evaluation, we conclude that the evaluated methods are both scalable and useful. Specifically, for a small number of reference points, the clustering-based methods outperformed the standard random selection of the original MLM formulation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge