Impatient Bandits: Optimizing for the Long-Term Without Delay

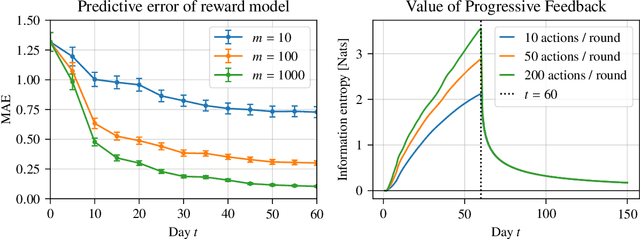
Increasingly, recommender systems are tasked with improving users' long-term satisfaction. In this context, we study a content exploration task, which we formalize as a bandit problem with delayed rewards. There is an apparent trade-off in choosing the learning signal: waiting for the full reward to become available might take several weeks, slowing the rate of learning, whereas using short-term proxy rewards reflects the actual long-term goal only imperfectly. First, we develop a predictive model of delayed rewards that incorporates all information obtained to date. Rewards as well as shorter-term surrogate outcomes are combined through a Bayesian filter to obtain a probabilistic belief. Second, we devise a bandit algorithm that quickly learns to identify content aligned with long-term success using this new predictive model. We prove a regret bound for our algorithm that depends on the \textit{Value of Progressive Feedback}, an information theoretic metric that captures the quality of short-term leading indicators that are observed prior to the long-term reward. We apply our approach to a podcast recommendation problem, where we seek to recommend shows that users engage with repeatedly over two months. We empirically validate that our approach significantly outperforms methods that optimize for short-term proxies or rely solely on delayed rewards, as demonstrated by an A/B test in a recommendation system that serves hundreds of millions of users.

Adaptive RKHS Fourier Features for Compositional Gaussian Process Models

Deep Gaussian Processes (DGPs) leverage a compositional structure to model non-stationary processes. DGPs typically rely on local inducing point approximations across intermediate GP layers. Recent advances in DGP inference have shown that incorporating global Fourier features from Reproducing Kernel Hilbert Space (RKHS) can enhance the DGPs' capability to capture complex non-stationary patterns. This paper extends the use of these features to compositional GPs involving linear transformations. In particular, we introduce Ordinary Differential Equation (ODE) -based RKHS Fourier features that allow for adaptive amplitude and phase modulation through convolution operations. This convolutional formulation relates our work to recently proposed deep latent force models, a multi-layer structure designed for modelling nonlinear dynamical systems. By embedding these adjustable RKHS Fourier features within a doubly stochastic variational inference framework, our model exhibits improved predictive performance across various regression tasks.

Deep Latent Force Models: ODE-based Process Convolutions for Bayesian Deep Learning

Effectively modeling phenomena present in highly nonlinear dynamical systems whilst also accurately quantifying uncertainty is a challenging task, which often requires problem-specific techniques. We outline the deep latent force model (DLFM), a domain-agnostic approach to tackling this problem, which consists of a deep Gaussian process architecture where the kernel at each layer is derived from an ordinary differential equation using the framework of process convolutions. Two distinct formulations of the DLFM are presented which utilise weight-space and variational inducing points-based Gaussian process approximations, both of which are amenable to doubly stochastic variational inference. We provide evidence that our model is capable of capturing highly nonlinear behaviour in real-world multivariate time series data. In addition, we find that our approach achieves comparable performance to a number of other probabilistic models on benchmark regression tasks. We also empirically assess the negative impact of the inducing points framework on the extrapolation capabilities of LFM-based models.