Recyclable Gaussian Processes
Paper and Code
Oct 06, 2020

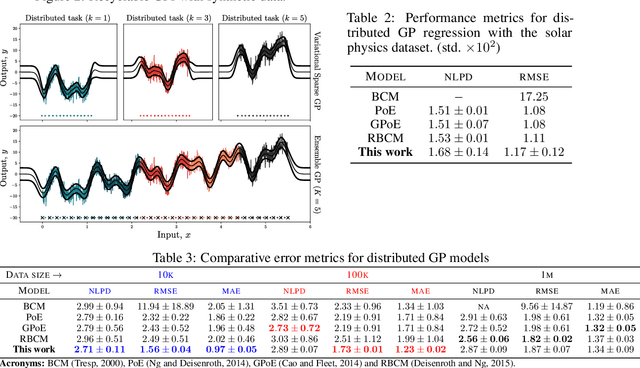
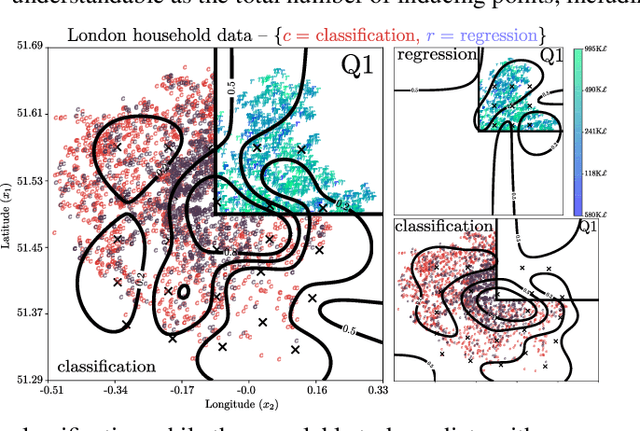
We present a new framework for recycling independent variational approximations to Gaussian processes. The main contribution is the construction of variational ensembles given a dictionary of fitted Gaussian processes without revisiting any subset of observations. Our framework allows for regression, classification and heterogeneous tasks, i.e. mix of continuous and discrete variables over the same input domain. We exploit infinite-dimensional integral operators based on the Kullback-Leibler divergence between stochastic processes to re-combine arbitrary amounts of variational sparse approximations with different complexity, likelihood model and location of the pseudo-inputs. Extensive results illustrate the usability of our framework in large-scale distributed experiments, also compared with the exact inference models in the literature.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge