Modular Gaussian Processes for Transfer Learning
Paper and Code
Oct 26, 2021
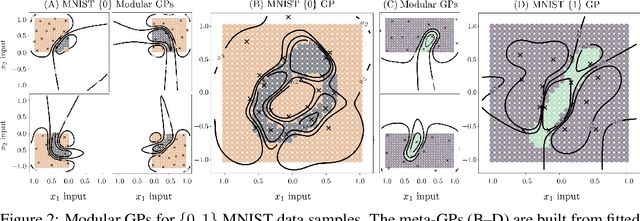
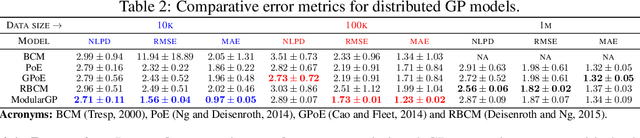
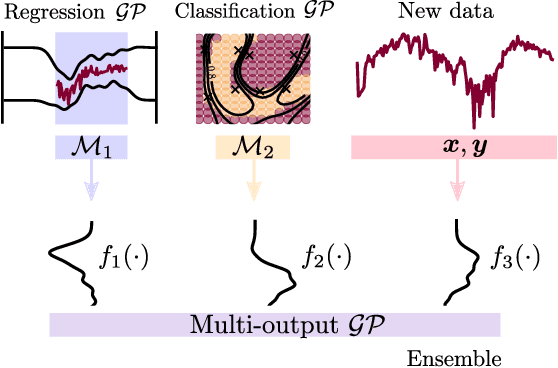
We present a framework for transfer learning based on modular variational Gaussian processes (GP). We develop a module-based method that having a dictionary of well fitted GPs, one could build ensemble GP models without revisiting any data. Each model is characterised by its hyperparameters, pseudo-inputs and their corresponding posterior densities. Our method avoids undesired data centralisation, reduces rising computational costs and allows the transfer of learned uncertainty metrics after training. We exploit the augmentation of high-dimensional integral operators based on the Kullback-Leibler divergence between stochastic processes to introduce an efficient lower bound under all the sparse variational GPs, with different complexity and even likelihood distribution. The method is also valid for multi-output GPs, learning correlations a posteriori between independent modules. Extensive results illustrate the usability of our framework in large-scale and multi-task experiments, also compared with the exact inference methods in the literature.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge