Privacy-preserving parametric inference: a case for robust statistics
Paper and Code
Nov 22, 2019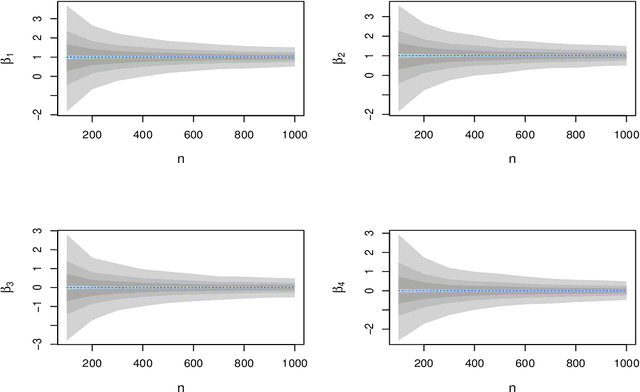
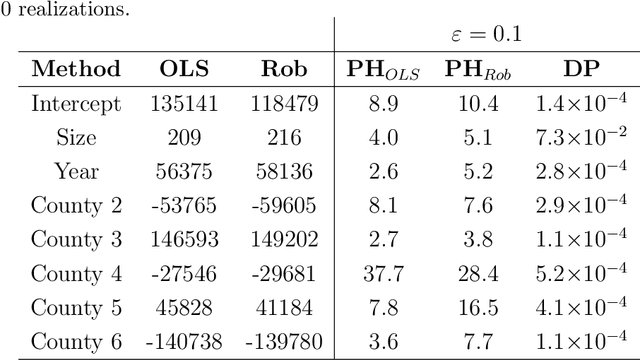
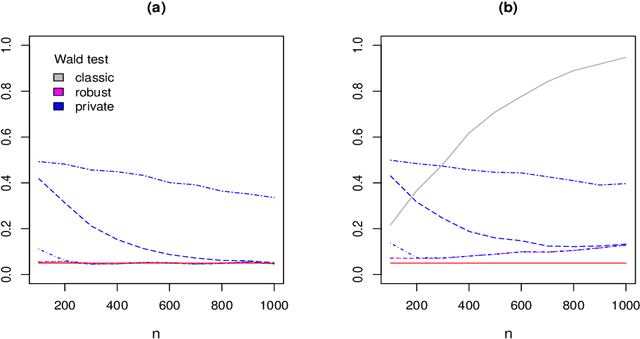
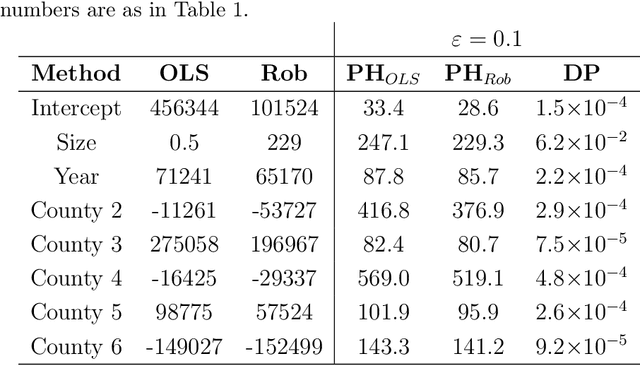
Differential privacy is a cryptographically-motivated approach to privacy that has become a very active field of research over the last decade in theoretical computer science and machine learning. In this paradigm one assumes there is a trusted curator who holds the data of individuals in a database and the goal of privacy is to simultaneously protect individual data while allowing the release of global characteristics of the database. In this setting we introduce a general framework for parametric inference with differential privacy guarantees. We first obtain differentially private estimators based on bounded influence M-estimators by leveraging their gross-error sensitivity in the calibration of a noise term added to them in order to ensure privacy. We then show how a similar construction can also be applied to construct differentially private test statistics analogous to the Wald, score and likelihood ratio tests. We provide statistical guarantees for all our proposals via an asymptotic analysis. An interesting consequence of our results is to further clarify the connection between differential privacy and robust statistics. In particular, we demonstrate that differential privacy is a weaker stability requirement than infinitesimal robustness, and show that robust M-estimators can be easily randomized in order to guarantee both differential privacy and robustness towards the presence of contaminated data. We illustrate our results both on simulated and real data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge