Francesco Trovò
LeakSealer: A Semisupervised Defense for LLMs Against Prompt Injection and Leakage Attacks
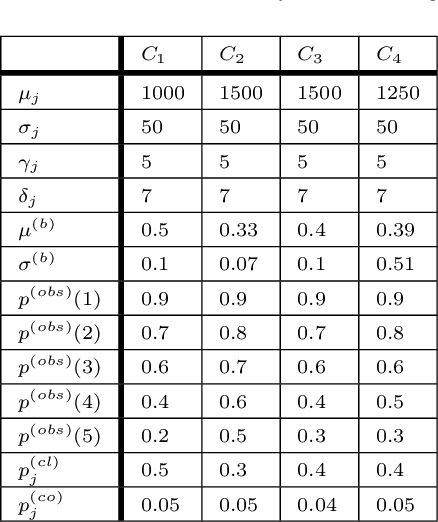
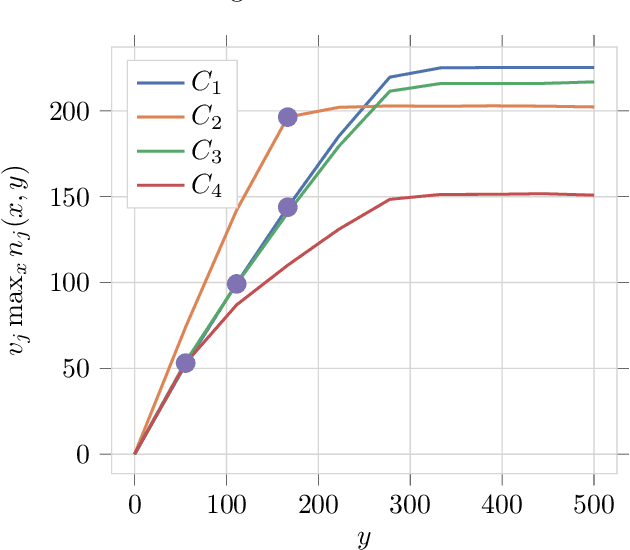
Aug 01, 2025Abstract:The generalization capabilities of Large Language Models (LLMs) have led to their widespread deployment across various applications. However, this increased adoption has introduced several security threats, notably in the forms of jailbreaking and data leakage attacks. Additionally, Retrieval Augmented Generation (RAG), while enhancing context-awareness in LLM responses, has inadvertently introduced vulnerabilities that can result in the leakage of sensitive information. Our contributions are twofold. First, we introduce a methodology to analyze historical interaction data from an LLM system, enabling the generation of usage maps categorized by topics (including adversarial interactions). This approach further provides forensic insights for tracking the evolution of jailbreaking attack patterns. Second, we propose LeakSealer, a model-agnostic framework that combines static analysis for forensic insights with dynamic defenses in a Human-In-The-Loop (HITL) pipeline. This technique identifies topic groups and detects anomalous patterns, allowing for proactive defense mechanisms. We empirically evaluate LeakSealer under two scenarios: (1) jailbreak attempts, employing a public benchmark dataset, and (2) PII leakage, supported by a curated dataset of labeled LLM interactions. In the static setting, LeakSealer achieves the highest precision and recall on the ToxicChat dataset when identifying prompt injection. In the dynamic setting, PII leakage detection achieves an AUPRC of $0.97$, significantly outperforming baselines such as Llama Guard.
Thompson Sampling-like Algorithms for Stochastic Rising Bandits
May 17, 2025Abstract:Stochastic rising rested bandit (SRRB) is a setting where the arms' expected rewards increase as they are pulled. It models scenarios in which the performances of the different options grow as an effect of an underlying learning process (e.g., online model selection). Even if the bandit literature provides specifically crafted algorithms based on upper-confidence bounds for such a setting, no study about Thompson sampling TS-like algorithms has been performed so far. The strong regularity of the expected rewards in the SRRB setting suggests that specific instances may be tackled effectively using adapted and sliding-window TS approaches. This work provides novel regret analyses for such algorithms in SRRBs, highlighting the challenges and providing new technical tools of independent interest. Our results allow us to identify under which assumptions TS-like algorithms succeed in achieving sublinear regret and which properties of the environment govern the complexity of the regret minimization problem when approached with TS. Furthermore, we provide a regret lower bound based on a complexity index we introduce. Finally, we conduct numerical simulations comparing TS-like algorithms with state-of-the-art approaches for SRRBs in synthetic and real-world settings.
Sliding-Window Thompson Sampling for Non-Stationary Settings
Sep 08, 2024Abstract:$\textit{Restless Bandits}$ describe sequential decision-making problems in which the rewards evolve with time independently from the actions taken by the policy-maker. It has been shown that classical Bandit algorithms fail when the underlying environment is changing, making clear that in order to tackle more challenging scenarios specifically crafted algorithms are needed. In this paper, extending and correcting the work by \cite{trovo2020sliding}, we analyze two Thompson-Sampling inspired algorithms, namely $\texttt{BETA-SWTS}$ and $\texttt{$\gamma$-SWGTS}$, introduced to face the additional complexity given by the non-stationary nature of the settings; in particular we derive a general formulation for the regret in $\textit{any}$ arbitrary restless environment for both Bernoulli and Subgaussian rewards, and, through the introduction of new quantities, we delve in what contribution lays the deeper foundations of the error made by the algorithms. Finally, we infer from the general formulation the regret for two of the most common non-stationary settings: the $\textit{Abruptly Changing}$ and the $\textit{Smoothly Changing}$ environments.
Stochastic Rising Bandits
Dec 07, 2022Abstract:This paper is in the field of stochastic Multi-Armed Bandits (MABs), i.e., those sequential selection techniques able to learn online using only the feedback given by the chosen option (a.k.a. arm). We study a particular case of the rested and restless bandits in which the arms' expected payoff is monotonically non-decreasing. This characteristic allows designing specifically crafted algorithms that exploit the regularity of the payoffs to provide tight regret bounds. We design an algorithm for the rested case (R-ed-UCB) and one for the restless case (R-less-UCB), providing a regret bound depending on the properties of the instance and, under certain circumstances, of $\widetilde{\mathcal{O}}(T^{\frac{2}{3}})$. We empirically compare our algorithms with state-of-the-art methods for non-stationary MABs over several synthetically generated tasks and an online model selection problem for a real-world dataset. Finally, using synthetic and real-world data, we illustrate the effectiveness of the proposed approaches compared with state-of-the-art algorithms for the non-stationary bandits.
* Corrected definition of "cumulative increment" (Equation 2) and efficient update (Appendix D)
Dynamic Pricing with Volume Discounts in Online Settings
Nov 17, 2022Abstract:According to the main international reports, more pervasive industrial and business-process automation, thanks to machine learning and advanced analytic tools, will unlock more than 14 trillion USD worldwide annually by 2030. In the specific case of pricing problems-which constitute the class of problems we investigate in this paper-, the estimated unlocked value will be about 0.5 trillion USD per year. In particular, this paper focuses on pricing in e-commerce when the objective function is profit maximization and only transaction data are available. This setting is one of the most common in real-world applications. Our work aims to find a pricing strategy that allows defining optimal prices at different volume thresholds to serve different classes of users. Furthermore, we face the major challenge, common in real-world settings, of dealing with limited data available. We design a two-phase online learning algorithm, namely PVD-B, capable of exploiting the data incrementally in an online fashion. The algorithm first estimates the demand curve and retrieves the optimal average price, and subsequently it offers discounts to differentiate the prices for each volume threshold. We ran a real-world 4-month-long A/B testing experiment in collaboration with an Italian e-commerce company, in which our algorithm PVD-B-corresponding to A configuration-has been compared with human pricing specialists-corresponding to B configuration. At the end of the experiment, our algorithm produced a total turnover of about 300 KEuros, outperforming the B configuration performance by about 55%. The Italian company we collaborated with decided to adopt our algorithm for more than 1,200 products since January 2022.
Multi-Armed Bandit Problem with Temporally-Partitioned Rewards: When Partial Feedback Counts
Jun 01, 2022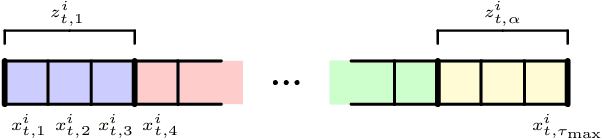
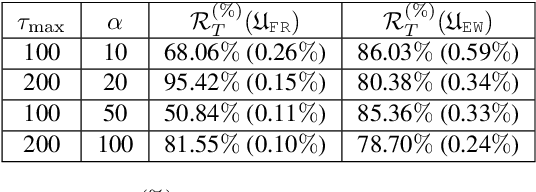
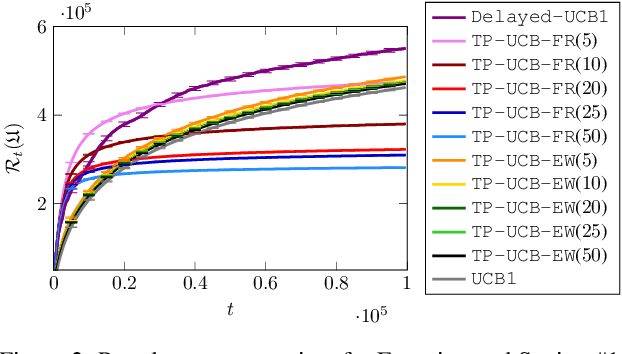
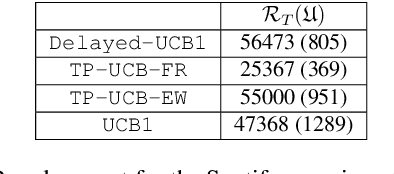
Abstract:There is a rising interest in industrial online applications where data becomes available sequentially. Inspired by the recommendation of playlists to users where their preferences can be collected during the listening of the entire playlist, we study a novel bandit setting, namely Multi-Armed Bandit with Temporally-Partitioned Rewards (TP-MAB), in which the stochastic reward associated with the pull of an arm is partitioned over a finite number of consecutive rounds following the pull. This setting, unexplored so far to the best of our knowledge, is a natural extension of delayed-feedback bandits to the case in which rewards may be dilated over a finite-time span after the pull instead of being fully disclosed in a single, potentially delayed round. We provide two algorithms to address TP-MAB problems, namely, TP-UCB-FR and TP-UCB-EW, which exploit the partial information disclosed by the reward collected over time. We show that our algorithms provide better asymptotical regret upper bounds than delayed-feedback bandit algorithms when a property characterizing a broad set of reward structures of practical interest, namely alpha-smoothness, holds. We also empirically evaluate their performance across a wide range of settings, both synthetically generated and from a real-world media recommendation problem.
ARLO: A Framework for Automated Reinforcement Learning
May 20, 2022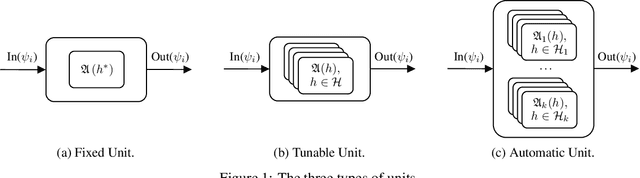

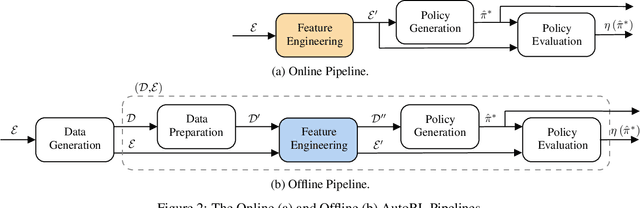
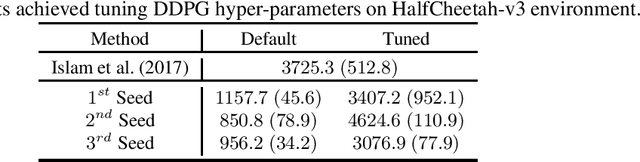
Abstract:Automated Reinforcement Learning (AutoRL) is a relatively new area of research that is gaining increasing attention. The objective of AutoRL consists in easing the employment of Reinforcement Learning (RL) techniques for the broader public by alleviating some of its main challenges, including data collection, algorithm selection, and hyper-parameter tuning. In this work, we propose a general and flexible framework, namely ARLO: Automated Reinforcement Learning Optimizer, to construct automated pipelines for AutoRL. Based on this, we propose a pipeline for offline and one for online RL, discussing the components, interaction, and highlighting the difference between the two settings. Furthermore, we provide a Python implementation of such pipelines, released as an open-source library. Our implementation has been tested on an illustrative LQG domain and on classic MuJoCo environments, showing the ability to reach competitive performances requiring limited human intervention. We also showcase the full pipeline on a realistic dam environment, automatically performing the feature selection and the model generation tasks.
Safe Online Bid Optimization with Return-On-Investment and Budget Constraints subject to Uncertainty
Jan 18, 2022Abstract:In online marketing, the advertisers' goal is usually a tradeoff between achieving high volumes and high profitability. The companies' business units customarily address this tradeoff by maximizing the volumes while guaranteeing a lower bound to the Return On Investment (ROI). This paper investigates combinatorial bandit algorithms for the bid optimization of advertising campaigns subject to uncertain budget and ROI constraints. We study the nature of both the optimization and learning problems. In particular, when focusing on the optimization problem without uncertainty, we show that it is inapproximable within any factor unless P=NP, and we provide a pseudo-polynomial-time algorithm that achieves an optimal solution. When considering uncertainty, we prove that no online learning algorithm can violate the (ROI or budget) constraints during the learning process a sublinear number of times while guaranteeing a sublinear pseudo-regret. Thus, we provide an algorithm, namely GCB, guaranteeing sublinear regret at the cost of a potentially linear number of constraints violations. We also design its safe version, namely GCB_{safe}, guaranteeing w.h.p. a constant upper bound on the number of constraints violations at the cost of a linear pseudo-regret. More interestingly, we provide an algorithm, namely GCB_{safe}(\psi,\phi), guaranteeing both sublinear pseudo-regret and safety w.h.p. at the cost of accepting tolerances \psi and \phi in the satisfaction of the ROI and budget constraints, respectively. This algorithm actually mitigates the risks due to the constraints violations without precluding the convergence to the optimal solution. Finally, we experimentally compare our algorithms in terms of pseudo-regret/constraint-violation tradeoff in settings generated from real-world data, showing the importance of adopting safety constraints in practice and the effectiveness of our algorithms.
Adapting Bandit Algorithms for Settings with Sequentially Available Arms
Sep 30, 2021
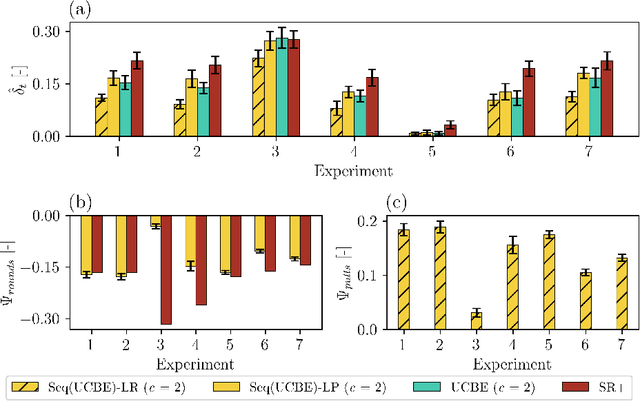
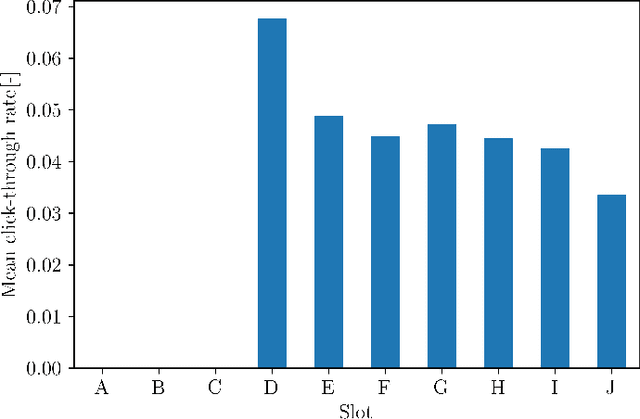
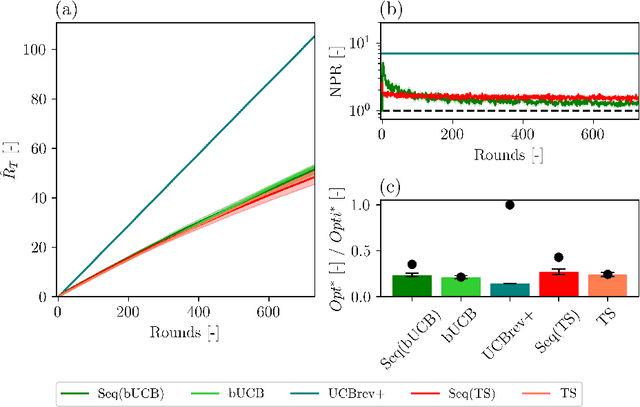
Abstract:Although the classical version of the Multi-Armed Bandits (MAB) framework has been applied successfully to several practical problems, in many real-world applications, the possible actions are not presented to the learner simultaneously, such as in the Internet campaign management and environmental monitoring settings. Instead, in such applications, a set of options is presented sequentially to the learner within a time span, and this process is repeated throughout a time horizon. At each time, the learner is asked whether to select the proposed option or not. We define this scenario as the Sequential Pull/No-pull Bandit setting, and we propose a meta-algorithm, namely Sequential Pull/No-pull for MAB (Seq), to adapt any classical MAB policy to better suit this setting for both the regret minimization and best-arm identification problems. By allowing the selection of multiple arms within a round, the proposed meta-algorithm gathers more information, especially in the first rounds, characterized by a high uncertainty in the arms estimate value. At the same time, the adapted algorithms provide the same theoretical guarantees as the classical policy employed. The Seq meta-algorithm was extensively tested and compared with classical MAB policies on synthetic and real-world datasets from advertising and environmental monitoring applications, highlighting its good empirical performances.
Online Joint Bid/Daily Budget Optimization of Internet Advertising Campaigns
Mar 03, 2020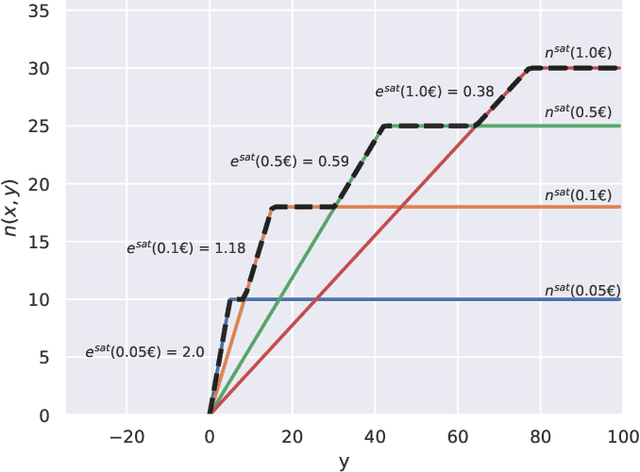
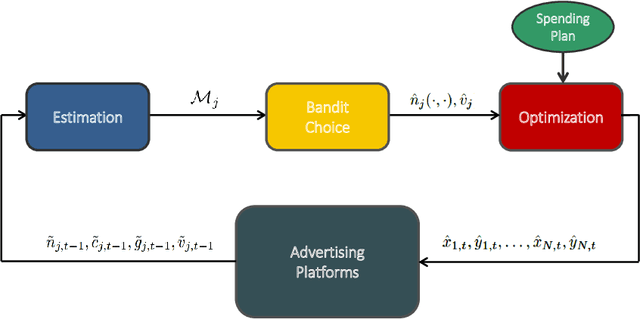
Abstract:Pay-per-click advertising includes various formats (\emph{e.g.}, search, contextual, social) with a total investment of more than 200 billion USD per year worldwide. An advertiser is given a daily budget to allocate over several, even thousands, campaigns, mainly distinguishing for the ad, target, or channel. Furthermore, publishers choose the ads to display and how to allocate them employing auctioning mechanisms, in which every day the advertisers set for each campaign a bid corresponding to the maximum amount of money per click they are willing to pay and the fraction of the daily budget to invest. In this paper, we study the problem of automating the online joint bid/daily budget optimization of pay-per-click advertising campaigns over multiple channels. We formulate our problem as a combinatorial semi-bandit problem, which requires solving a special case of the Multiple-Choice Knapsack problem every day. Furthermore, for every campaign, we capture the dependency of the number of clicks on the bid and daily budget by Gaussian Processes, thus requiring mild assumptions on the regularity of these functions. We design four algorithms and show that they suffer from a regret that is upper bounded with high probability as O(sqrt{T}), where T is the time horizon of the learning process. We experimentally evaluate our algorithms with synthetic settings generated from real data from Yahoo!, and we present the results of the adoption of our algorithms in a real-world application with a daily average spent of 1,000 Euros for more than one year.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge