Better Regret Rates in Bilateral Trade via Sublinear Budget Violation

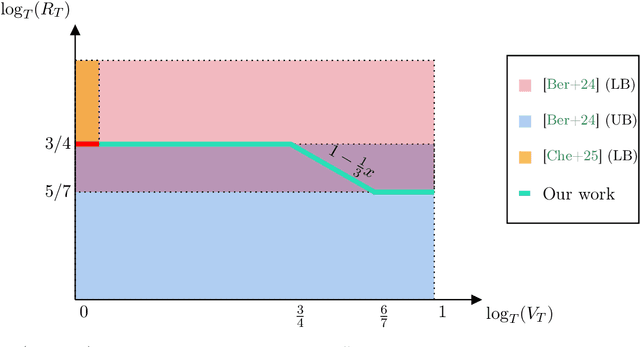
Bilateral trade is a central problem in algorithmic economics, and recent work has explored how to design trading mechanisms using no-regret learning algorithms. However, no-regret learning is impossible when budget balance has to be enforced at each time step. Bernasconi et al. [Ber+24] show how this impossibility can be circumvented by relaxing the budget balance constraint to hold only globally over all time steps. In particular, they design an algorithm achieving regret of the order of $\tilde O(T^{3/4})$ and provide a lower bound of $\Omega(T^{5/7})$. In this work, we interpolate between these two extremes by studying how the optimal regret rate varies with the allowed violation of the global budget balance constraint. Specifically, we design an algorithm that, by violating the constraint by at most $T^{\beta}$ for any given $\beta \in [\frac{3}{4}, \frac{6}{7}]$, attains regret $\tilde O(T^{1 - \beta/3})$. We complement this result with a matching lower bound, thus fully characterizing the trade-off between regret and budget violation. Our results show that both the $\tilde O(T^{3/4})$ upper bound in the global budget balance case and the $\Omega(T^{5/7})$ lower bound under unconstrained budget balance violation obtained by Bernasconi et al. [Ber+24] are tight.

No-Regret Learning Under Adversarial Resource Constraints: A Spending Plan Is All You Need!

We study online decision making problems under resource constraints, where both reward and cost functions are drawn from distributions that may change adversarially over time. We focus on two canonical settings: $(i)$ online resource allocation where rewards and costs are observed before action selection, and $(ii)$ online learning with resource constraints where they are observed after action selection, under full feedback or bandit feedback. It is well known that achieving sublinear regret in these settings is impossible when reward and cost distributions may change arbitrarily over time. To address this challenge, we analyze a framework in which the learner is guided by a spending plan--a sequence prescribing expected resource usage across rounds. We design general (primal-)dual methods that achieve sublinear regret with respect to baselines that follow the spending plan. Crucially, the performance of our algorithms improves when the spending plan ensures a well-balanced distribution of the budget across rounds. We additionally provide a robust variant of our methods to handle worst-case scenarios where the spending plan is highly imbalanced. To conclude, we study the regret of our algorithms when competing against benchmarks that deviate from the prescribed spending plan.

Data-Dependent Regret Bounds for Constrained MABs

This paper initiates the study of data-dependent regret bounds in constrained MAB settings. These bounds depend on the sequence of losses that characterize the problem instance. Thus, they can be much smaller than classical $\widetilde{\mathcal{O}}(\sqrt{T})$ regret bounds, while being equivalent to them in the worst case. Despite this, data-dependent regret bounds have been completely overlooked in constrained MAB settings. The goal of this paper is to answer the following question: Can data-dependent regret bounds be derived in the presence of constraints? We answer this question affirmatively in constrained MABs with adversarial losses and stochastic constraints. Specifically, our main focus is on the most challenging and natural settings with hard constraints, where the learner must ensure that the constraints are always satisfied with high probability. We design an algorithm with a regret bound consisting of two data-dependent terms. The first term captures the difficulty of satisfying the constraints, while the second one encodes the complexity of learning independently of the presence of constraints. We also prove a lower bound showing that these two terms are not artifacts of our specific approach and analysis, but rather the fundamental components that inherently characterize the complexities of the problem. Finally, in designing our algorithm, we also derive some novel results in the related (and easier) soft constraints settings, which may be of independent interest.

Regret Minimization for Piecewise Linear Rewards: Contracts, Auctions, and Beyond

Most microeconomic models of interest involve optimizing a piecewise linear function. These include contract design in hidden-action principal-agent problems, selling an item in posted-price auctions, and bidding in first-price auctions. When the relevant model parameters are unknown and determined by some (unknown) probability distributions, the problem becomes learning how to optimize an unknown and stochastic piecewise linear reward function. Such a problem is usually framed within an online learning framework, where the decision-maker (learner) seeks to minimize the regret of not knowing an optimal decision in hindsight. This paper introduces a general online learning framework that offers a unified approach to tackle regret minimization for piecewise linear rewards, under a suitable monotonicity assumption commonly satisfied by microeconomic models. We design a learning algorithm that attains a regret of $\widetilde{O}(\sqrt{nT})$, where $n$ is the number of ``pieces'' of the reward function and $T$ is the number of rounds. This result is tight when $n$ is \emph{small} relative to $T$, specifically when $n \leq T^{1/3}$. Our algorithm solves two open problems in the literature on learning in microeconomic settings. First, it shows that the $\widetilde{O}(T^{2/3})$ regret bound obtained by Zhu et al. [Zhu+23] for learning optimal linear contracts in hidden-action principal-agent problems is not tight when the number of agent's actions is small relative to $T$. Second, our algorithm demonstrates that, in the problem of learning to set prices in posted-price auctions, it is possible to attain suitable (and desirable) instance-independent regret bounds, addressing an open problem posed by Cesa-Bianchi et al. [CBCP19].

Best-of-Both-Worlds Policy Optimization for CMDPs with Bandit Feedback

We study online learning in constrained Markov decision processes (CMDPs) in which rewards and constraints may be either stochastic or adversarial. In such settings, Stradi et al.(2024) proposed the first best-of-both-worlds algorithm able to seamlessly handle stochastic and adversarial constraints, achieving optimal regret and constraint violation bounds in both cases. This algorithm suffers from two major drawbacks. First, it only works under full feedback, which severely limits its applicability in practice. Moreover, it relies on optimizing over the space of occupancy measures, which requires solving convex optimization problems, an highly inefficient task. In this paper, we provide the first best-of-both-worlds algorithm for CMDPs with bandit feedback. Specifically, when the constraints are stochastic, the algorithm achieves $\widetilde{\mathcal{O}}(\sqrt{T})$ regret and constraint violation, while, when they are adversarial, it attains $\widetilde{\mathcal{O}}(\sqrt{T})$ constraint violation and a tight fraction of the optimal reward. Moreover, our algorithm is based on a policy optimization approach, which is much more efficient than occupancy-measure-based methods.

Optimal Strong Regret and Violation in Constrained MDPs via Policy Optimization

We study online learning in \emph{constrained MDPs} (CMDPs), focusing on the goal of attaining sublinear strong regret and strong cumulative constraint violation. Differently from their standard (weak) counterparts, these metrics do not allow negative terms to compensate positive ones, raising considerable additional challenges. Efroni et al. (2020) were the first to propose an algorithm with sublinear strong regret and strong violation, by exploiting linear programming. Thus, their algorithm is highly inefficient, leaving as an open problem achieving sublinear bounds by means of policy optimization methods, which are much more efficient in practice. Very recently, Muller et al. (2024) have partially addressed this problem by proposing a policy optimization method that allows to attain $\widetilde{\mathcal{O}}(T^{0.93})$ strong regret/violation. This still leaves open the question of whether optimal bounds are achievable by using an approach of this kind. We answer such a question affirmatively, by providing an efficient policy optimization algorithm with $\widetilde{\mathcal{O}}(\sqrt{T})$ strong regret/violation. Our algorithm implements a primal-dual scheme that employs a state-of-the-art policy optimization approach for adversarial (unconstrained) MDPs as primal algorithm, and a UCB-like update for dual variables.

Learning Constrained Markov Decision Processes With Non-stationary Rewards and Constraints

In constrained Markov decision processes (CMDPs) with adversarial rewards and constraints, a well-known impossibility result prevents any algorithm from attaining both sublinear regret and sublinear constraint violation, when competing against a best-in-hindsight policy that satisfies constraints on average. In this paper, we show that this negative result can be eased in CMDPs with non-stationary rewards and constraints, by providing algorithms whose performances smoothly degrade as non-stationarity increases. Specifically, we propose algorithms attaining $\tilde{\mathcal{O}} (\sqrt{T} + C)$ regret and positive constraint violation under bandit feedback, where $C$ is a corruption value measuring the environment non-stationarity. This can be $\Theta(T)$ in the worst case, coherently with the impossibility result for adversarial CMDPs. First, we design an algorithm with the desired guarantees when $C$ is known. Then, in the case $C$ is unknown, we show how to obtain the same results by embedding such an algorithm in a general meta-procedure. This is of independent interest, as it can be applied to any non-stationary constrained online learning setting.

Learning Adversarial MDPs with Stochastic Hard Constraints

We study online learning problems in constrained Markov decision processes (CMDPs) with adversarial losses and stochastic hard constraints. We consider two different scenarios. In the first one, we address general CMDPs, where we design an algorithm that attains sublinear regret and cumulative positive constraints violation. In the second scenario, under the mild assumption that a policy strictly satisfying the constraints exists and is known to the learner, we design an algorithm that achieves sublinear regret while ensuring that the constraints are satisfied at every episode with high probability. To the best of our knowledge, our work is the first to study CMDPs involving both adversarial losses and hard constraints. Indeed, previous works either focus on much weaker soft constraints--allowing for positive violation to cancel out negative ones--or are restricted to stochastic losses. Thus, our algorithms can deal with general non-stationary environments subject to requirements much stricter than those manageable with state-of-the-art algorithms. This enables their adoption in a much wider range of real-world applications, ranging from autonomous driving to online advertising and recommender systems.

Markov Persuasion Processes: Learning to Persuade from Scratch

In Bayesian persuasion, an informed sender strategically discloses information to a receiver so as to persuade them to undertake desirable actions. Recently, a growing attention has been devoted to settings in which sender and receivers interact sequentially. Recently, Markov persuasion processes (MPPs) have been introduced to capture sequential scenarios where a sender faces a stream of myopic receivers in a Markovian environment. The MPPs studied so far in the literature suffer from issues that prevent them from being fully operational in practice, e.g., they assume that the sender knows receivers' rewards. We fix such issues by addressing MPPs where the sender has no knowledge about the environment. We design a learning algorithm for the sender, working with partial feedback. We prove that its regret with respect to an optimal information-disclosure policy grows sublinearly in the number of episodes, as it is the case for the loss in persuasiveness cumulated while learning. Moreover, we provide a lower bound for our setting matching the guarantees of our algorithm.

Learning Optimal Contracts: How to Exploit Small Action Spaces

We study principal-agent problems in which a principal commits to an outcome-dependent payment scheme -- called contract -- in order to induce an agent to take a costly, unobservable action leading to favorable outcomes. We consider a generalization of the classical (single-round) version of the problem in which the principal interacts with the agent by committing to contracts over multiple rounds. The principal has no information about the agent, and they have to learn an optimal contract by only observing the outcome realized at each round. We focus on settings in which the size of the agent's action space is small. We design an algorithm that learns an approximately-optimal contract with high probability in a number of rounds polynomial in the size of the outcome space, when the number of actions is constant. Our algorithm solves an open problem by Zhu et al.[2022]. Moreover, it can also be employed to provide a $\tilde{\mathcal{O}}(T^{4/5})$ regret bound in the related online learning setting in which the principal aims at maximizing their cumulative utility, thus considerably improving previously-known regret bounds.