Francesco Emanuele Stradi
No-Regret Learning Under Adversarial Resource Constraints: A Spending Plan Is All You Need!
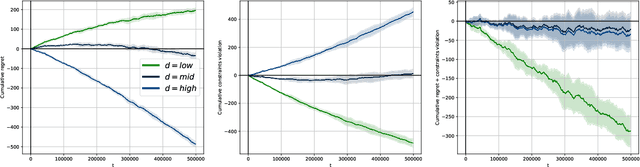
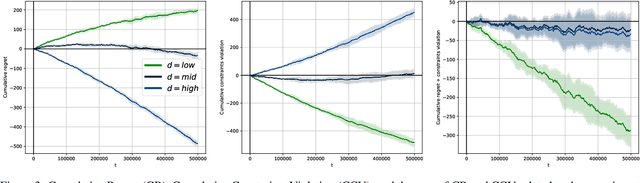
Jun 16, 2025Abstract:We study online decision making problems under resource constraints, where both reward and cost functions are drawn from distributions that may change adversarially over time. We focus on two canonical settings: $(i)$ online resource allocation where rewards and costs are observed before action selection, and $(ii)$ online learning with resource constraints where they are observed after action selection, under full feedback or bandit feedback. It is well known that achieving sublinear regret in these settings is impossible when reward and cost distributions may change arbitrarily over time. To address this challenge, we analyze a framework in which the learner is guided by a spending plan--a sequence prescribing expected resource usage across rounds. We design general (primal-)dual methods that achieve sublinear regret with respect to baselines that follow the spending plan. Crucially, the performance of our algorithms improves when the spending plan ensures a well-balanced distribution of the budget across rounds. We additionally provide a robust variant of our methods to handle worst-case scenarios where the spending plan is highly imbalanced. To conclude, we study the regret of our algorithms when competing against benchmarks that deviate from the prescribed spending plan.
Data-Dependent Regret Bounds for Constrained MABs
May 26, 2025Abstract:This paper initiates the study of data-dependent regret bounds in constrained MAB settings. These bounds depend on the sequence of losses that characterize the problem instance. Thus, they can be much smaller than classical $\widetilde{\mathcal{O}}(\sqrt{T})$ regret bounds, while being equivalent to them in the worst case. Despite this, data-dependent regret bounds have been completely overlooked in constrained MAB settings. The goal of this paper is to answer the following question: Can data-dependent regret bounds be derived in the presence of constraints? We answer this question affirmatively in constrained MABs with adversarial losses and stochastic constraints. Specifically, our main focus is on the most challenging and natural settings with hard constraints, where the learner must ensure that the constraints are always satisfied with high probability. We design an algorithm with a regret bound consisting of two data-dependent terms. The first term captures the difficulty of satisfying the constraints, while the second one encodes the complexity of learning independently of the presence of constraints. We also prove a lower bound showing that these two terms are not artifacts of our specific approach and analysis, but rather the fundamental components that inherently characterize the complexities of the problem. Finally, in designing our algorithm, we also derive some novel results in the related (and easier) soft constraints settings, which may be of independent interest.
Optimal Strong Regret and Violation in Constrained MDPs via Policy Optimization
Oct 03, 2024Abstract:We study online learning in \emph{constrained MDPs} (CMDPs), focusing on the goal of attaining sublinear strong regret and strong cumulative constraint violation. Differently from their standard (weak) counterparts, these metrics do not allow negative terms to compensate positive ones, raising considerable additional challenges. Efroni et al. (2020) were the first to propose an algorithm with sublinear strong regret and strong violation, by exploiting linear programming. Thus, their algorithm is highly inefficient, leaving as an open problem achieving sublinear bounds by means of policy optimization methods, which are much more efficient in practice. Very recently, Muller et al. (2024) have partially addressed this problem by proposing a policy optimization method that allows to attain $\widetilde{\mathcal{O}}(T^{0.93})$ strong regret/violation. This still leaves open the question of whether optimal bounds are achievable by using an approach of this kind. We answer such a question affirmatively, by providing an efficient policy optimization algorithm with $\widetilde{\mathcal{O}}(\sqrt{T})$ strong regret/violation. Our algorithm implements a primal-dual scheme that employs a state-of-the-art policy optimization approach for adversarial (unconstrained) MDPs as primal algorithm, and a UCB-like update for dual variables.
Best-of-Both-Worlds Policy Optimization for CMDPs with Bandit Feedback
Oct 03, 2024Abstract:We study online learning in constrained Markov decision processes (CMDPs) in which rewards and constraints may be either stochastic or adversarial. In such settings, Stradi et al.(2024) proposed the first best-of-both-worlds algorithm able to seamlessly handle stochastic and adversarial constraints, achieving optimal regret and constraint violation bounds in both cases. This algorithm suffers from two major drawbacks. First, it only works under full feedback, which severely limits its applicability in practice. Moreover, it relies on optimizing over the space of occupancy measures, which requires solving convex optimization problems, an highly inefficient task. In this paper, we provide the first best-of-both-worlds algorithm for CMDPs with bandit feedback. Specifically, when the constraints are stochastic, the algorithm achieves $\widetilde{\mathcal{O}}(\sqrt{T})$ regret and constraint violation, while, when they are adversarial, it attains $\widetilde{\mathcal{O}}(\sqrt{T})$ constraint violation and a tight fraction of the optimal reward. Moreover, our algorithm is based on a policy optimization approach, which is much more efficient than occupancy-measure-based methods.
A Primal-Dual Online Learning Approach for Dynamic Pricing of Sequentially Displayed Complementary Items under Sale Constraints
Jul 08, 2024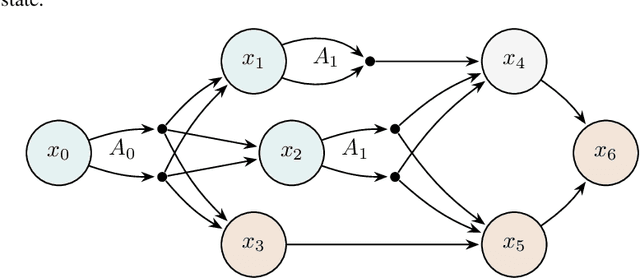

Abstract:We address the challenging problem of dynamically pricing complementary items that are sequentially displayed to customers. An illustrative example is the online sale of flight tickets, where customers navigate through multiple web pages. Initially, they view the ticket cost, followed by ancillary expenses such as insurance and additional luggage fees. Coherent pricing policies for complementary items are essential because optimizing the pricing of each item individually is ineffective. Our scenario also involves a sales constraint, which specifies a minimum number of items to sell, and uncertainty regarding customer demand curves. To tackle this problem, we originally formulate it as a Markov Decision Process with constraints. Leveraging online learning tools, we design a primal-dual online optimization algorithm. We empirically evaluate our approach using synthetic settings randomly generated from real-world data, covering various configurations from stationary to non-stationary, and compare its performance in terms of constraints violation and regret against well-known baselines optimizing each state singularly.
Learning Constrained Markov Decision Processes With Non-stationary Rewards and Constraints
May 23, 2024Abstract:In constrained Markov decision processes (CMDPs) with adversarial rewards and constraints, a well-known impossibility result prevents any algorithm from attaining both sublinear regret and sublinear constraint violation, when competing against a best-in-hindsight policy that satisfies constraints on average. In this paper, we show that this negative result can be eased in CMDPs with non-stationary rewards and constraints, by providing algorithms whose performances smoothly degrade as non-stationarity increases. Specifically, we propose algorithms attaining $\tilde{\mathcal{O}} (\sqrt{T} + C)$ regret and positive constraint violation under bandit feedback, where $C$ is a corruption value measuring the environment non-stationarity. This can be $\Theta(T)$ in the worst case, coherently with the impossibility result for adversarial CMDPs. First, we design an algorithm with the desired guarantees when $C$ is known. Then, in the case $C$ is unknown, we show how to obtain the same results by embedding such an algorithm in a general meta-procedure. This is of independent interest, as it can be applied to any non-stationary constrained online learning setting.
Learning Adversarial MDPs with Stochastic Hard Constraints
Mar 06, 2024Abstract:We study online learning problems in constrained Markov decision processes (CMDPs) with adversarial losses and stochastic hard constraints. We consider two different scenarios. In the first one, we address general CMDPs, where we design an algorithm that attains sublinear regret and cumulative positive constraints violation. In the second scenario, under the mild assumption that a policy strictly satisfying the constraints exists and is known to the learner, we design an algorithm that achieves sublinear regret while ensuring that the constraints are satisfied at every episode with high probability. To the best of our knowledge, our work is the first to study CMDPs involving both adversarial losses and hard constraints. Indeed, previous works either focus on much weaker soft constraints--allowing for positive violation to cancel out negative ones--or are restricted to stochastic losses. Thus, our algorithms can deal with general non-stationary environments subject to requirements much stricter than those manageable with state-of-the-art algorithms. This enables their adoption in a much wider range of real-world applications, ranging from autonomous driving to online advertising and recommender systems.
Markov Persuasion Processes: Learning to Persuade from Scratch
Feb 05, 2024Abstract:In Bayesian persuasion, an informed sender strategically discloses information to a receiver so as to persuade them to undertake desirable actions. Recently, a growing attention has been devoted to settings in which sender and receivers interact sequentially. Recently, Markov persuasion processes (MPPs) have been introduced to capture sequential scenarios where a sender faces a stream of myopic receivers in a Markovian environment. The MPPs studied so far in the literature suffer from issues that prevent them from being fully operational in practice, e.g., they assume that the sender knows receivers' rewards. We fix such issues by addressing MPPs where the sender has no knowledge about the environment. We design a learning algorithm for the sender, working with partial feedback. We prove that its regret with respect to an optimal information-disclosure policy grows sublinearly in the number of episodes, as it is the case for the loss in persuasiveness cumulated while learning. Moreover, we provide a lower bound for our setting matching the guarantees of our algorithm.
A Best-of-Both-Worlds Algorithm for Constrained MDPs with Long-Term Constraints
Apr 27, 2023
Abstract:We study online learning in episodic constrained Markov decision processes (CMDPs), where the goal of the learner is to collect as much reward as possible over the episodes, while guaranteeing that some long-term constraints are satisfied during the learning process. Rewards and constraints can be selected either stochastically or adversarially, and the transition function is not known to the learner. While online learning in classical unconstrained MDPs has received considerable attention over the last years, the setting of CMDPs is still largely unexplored. This is surprising, since in real-world applications, such as, e.g., autonomous driving, automated bidding, and recommender systems, there are usually additional constraints and specifications that an agent has to obey during the learning process. In this paper, we provide the first best-of-both-worlds algorithm for CMDPs with long-term constraints. Our algorithm is capable of handling settings in which rewards and constraints are selected either stochastically or adversarially, without requiring any knowledge of the underling process. Moreover, our algorithm matches state-of-the-art regret and constraint violation bounds for settings in which constraints are selected stochastically, while it is the first to provide guarantees in the case in which they are chosen adversarially.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge