A Unifying Framework for Online Optimization with Long-Term Constraints

We study online learning problems in which a decision maker has to take a sequence of decisions subject to $m$ long-term constraints. The goal of the decision maker is to maximize their total reward, while at the same time achieving small cumulative constraints violation across the $T$ rounds. We present the first best-of-both-world type algorithm for this general class of problems, with no-regret guarantees both in the case in which rewards and constraints are selected according to an unknown stochastic model, and in the case in which they are selected at each round by an adversary. Our algorithm is the first to provide guarantees in the adversarial setting with respect to the optimal fixed strategy that satisfies the long-term constraints. In particular, it guarantees a $\rho/(1+\rho)$ fraction of the optimal reward and sublinear regret, where $\rho$ is a feasibility parameter related to the existence of strictly feasible solutions. Our framework employs traditional regret minimizers as black-box components. Therefore, by instantiating it with an appropriate choice of regret minimizers it can handle the full-feedback as well as the bandit-feedback setting. Moreover, it allows the decision maker to seamlessly handle scenarios with non-convex rewards and constraints. We show how our framework can be applied in the context of budget-management mechanisms for repeated auctions in order to guarantee long-term constraints that are not packing (e.g., ROI constraints).

Multi-Armed Bandit Problem with Temporally-Partitioned Rewards: When Partial Feedback Counts

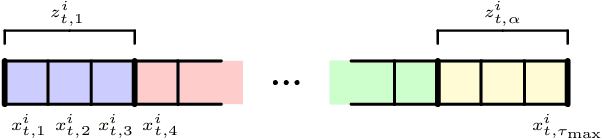
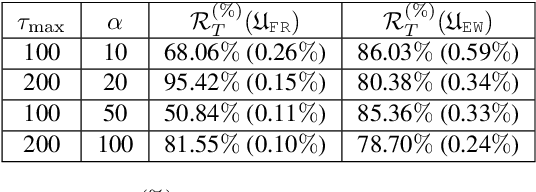
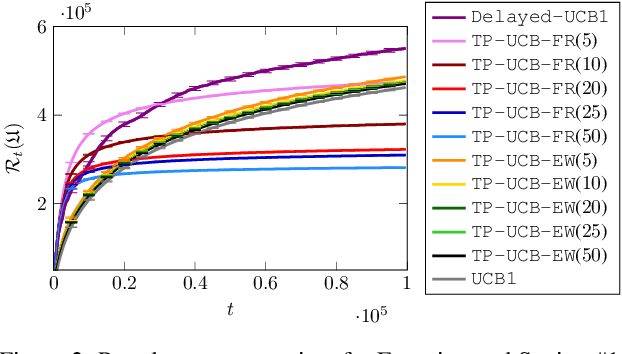
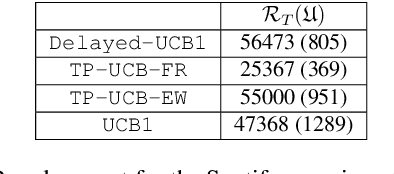
There is a rising interest in industrial online applications where data becomes available sequentially. Inspired by the recommendation of playlists to users where their preferences can be collected during the listening of the entire playlist, we study a novel bandit setting, namely Multi-Armed Bandit with Temporally-Partitioned Rewards (TP-MAB), in which the stochastic reward associated with the pull of an arm is partitioned over a finite number of consecutive rounds following the pull. This setting, unexplored so far to the best of our knowledge, is a natural extension of delayed-feedback bandits to the case in which rewards may be dilated over a finite-time span after the pull instead of being fully disclosed in a single, potentially delayed round. We provide two algorithms to address TP-MAB problems, namely, TP-UCB-FR and TP-UCB-EW, which exploit the partial information disclosed by the reward collected over time. We show that our algorithms provide better asymptotical regret upper bounds than delayed-feedback bandit algorithms when a property characterizing a broad set of reward structures of practical interest, namely alpha-smoothness, holds. We also empirically evaluate their performance across a wide range of settings, both synthetically generated and from a real-world media recommendation problem.

Safe Online Bid Optimization with Return-On-Investment and Budget Constraints subject to Uncertainty

In online marketing, the advertisers' goal is usually a tradeoff between achieving high volumes and high profitability. The companies' business units customarily address this tradeoff by maximizing the volumes while guaranteeing a lower bound to the Return On Investment (ROI). This paper investigates combinatorial bandit algorithms for the bid optimization of advertising campaigns subject to uncertain budget and ROI constraints. We study the nature of both the optimization and learning problems. In particular, when focusing on the optimization problem without uncertainty, we show that it is inapproximable within any factor unless P=NP, and we provide a pseudo-polynomial-time algorithm that achieves an optimal solution. When considering uncertainty, we prove that no online learning algorithm can violate the (ROI or budget) constraints during the learning process a sublinear number of times while guaranteeing a sublinear pseudo-regret. Thus, we provide an algorithm, namely GCB, guaranteeing sublinear regret at the cost of a potentially linear number of constraints violations. We also design its safe version, namely GCB_{safe}, guaranteeing w.h.p. a constant upper bound on the number of constraints violations at the cost of a linear pseudo-regret. More interestingly, we provide an algorithm, namely GCB_{safe}(\psi,\phi), guaranteeing both sublinear pseudo-regret and safety w.h.p. at the cost of accepting tolerances \psi and \phi in the satisfaction of the ROI and budget constraints, respectively. This algorithm actually mitigates the risks due to the constraints violations without precluding the convergence to the optimal solution. Finally, we experimentally compare our algorithms in terms of pseudo-regret/constraint-violation tradeoff in settings generated from real-world data, showing the importance of adopting safety constraints in practice and the effectiveness of our algorithms.