Alessandro Nuara
Dynamic Pricing with Volume Discounts in Online Settings
Nov 17, 2022Abstract:According to the main international reports, more pervasive industrial and business-process automation, thanks to machine learning and advanced analytic tools, will unlock more than 14 trillion USD worldwide annually by 2030. In the specific case of pricing problems-which constitute the class of problems we investigate in this paper-, the estimated unlocked value will be about 0.5 trillion USD per year. In particular, this paper focuses on pricing in e-commerce when the objective function is profit maximization and only transaction data are available. This setting is one of the most common in real-world applications. Our work aims to find a pricing strategy that allows defining optimal prices at different volume thresholds to serve different classes of users. Furthermore, we face the major challenge, common in real-world settings, of dealing with limited data available. We design a two-phase online learning algorithm, namely PVD-B, capable of exploiting the data incrementally in an online fashion. The algorithm first estimates the demand curve and retrieves the optimal average price, and subsequently it offers discounts to differentiate the prices for each volume threshold. We ran a real-world 4-month-long A/B testing experiment in collaboration with an Italian e-commerce company, in which our algorithm PVD-B-corresponding to A configuration-has been compared with human pricing specialists-corresponding to B configuration. At the end of the experiment, our algorithm produced a total turnover of about 300 KEuros, outperforming the B configuration performance by about 55%. The Italian company we collaborated with decided to adopt our algorithm for more than 1,200 products since January 2022.
Safe Online Bid Optimization with Return-On-Investment and Budget Constraints subject to Uncertainty
Jan 18, 2022Abstract:In online marketing, the advertisers' goal is usually a tradeoff between achieving high volumes and high profitability. The companies' business units customarily address this tradeoff by maximizing the volumes while guaranteeing a lower bound to the Return On Investment (ROI). This paper investigates combinatorial bandit algorithms for the bid optimization of advertising campaigns subject to uncertain budget and ROI constraints. We study the nature of both the optimization and learning problems. In particular, when focusing on the optimization problem without uncertainty, we show that it is inapproximable within any factor unless P=NP, and we provide a pseudo-polynomial-time algorithm that achieves an optimal solution. When considering uncertainty, we prove that no online learning algorithm can violate the (ROI or budget) constraints during the learning process a sublinear number of times while guaranteeing a sublinear pseudo-regret. Thus, we provide an algorithm, namely GCB, guaranteeing sublinear regret at the cost of a potentially linear number of constraints violations. We also design its safe version, namely GCB_{safe}, guaranteeing w.h.p. a constant upper bound on the number of constraints violations at the cost of a linear pseudo-regret. More interestingly, we provide an algorithm, namely GCB_{safe}(\psi,\phi), guaranteeing both sublinear pseudo-regret and safety w.h.p. at the cost of accepting tolerances \psi and \phi in the satisfaction of the ROI and budget constraints, respectively. This algorithm actually mitigates the risks due to the constraints violations without precluding the convergence to the optimal solution. Finally, we experimentally compare our algorithms in terms of pseudo-regret/constraint-violation tradeoff in settings generated from real-world data, showing the importance of adopting safety constraints in practice and the effectiveness of our algorithms.
Online Joint Bid/Daily Budget Optimization of Internet Advertising Campaigns
Mar 03, 2020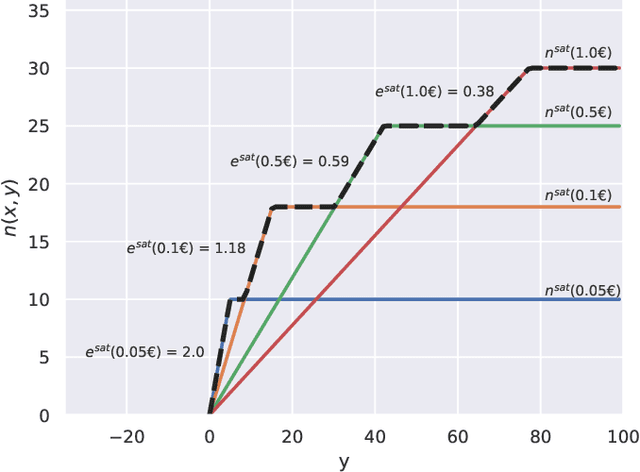
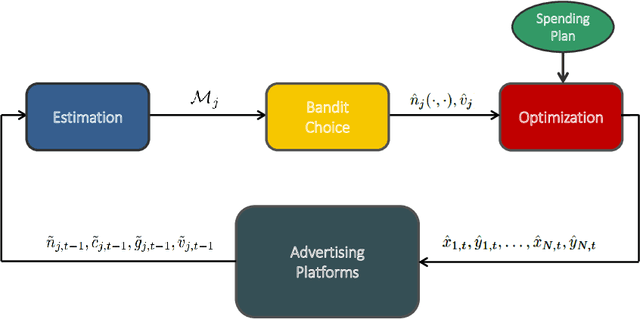
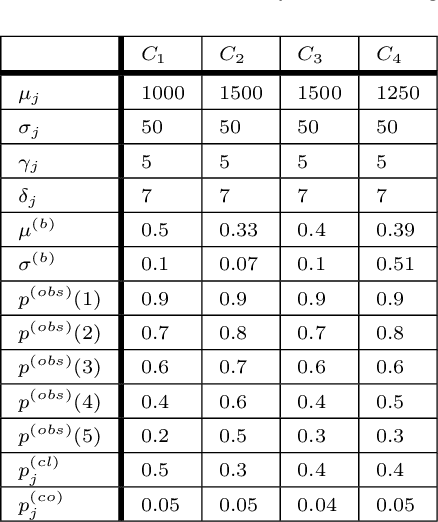
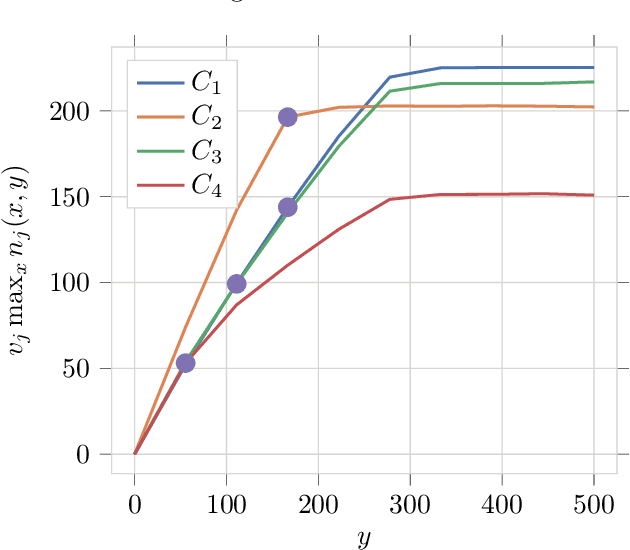
Abstract:Pay-per-click advertising includes various formats (\emph{e.g.}, search, contextual, social) with a total investment of more than 200 billion USD per year worldwide. An advertiser is given a daily budget to allocate over several, even thousands, campaigns, mainly distinguishing for the ad, target, or channel. Furthermore, publishers choose the ads to display and how to allocate them employing auctioning mechanisms, in which every day the advertisers set for each campaign a bid corresponding to the maximum amount of money per click they are willing to pay and the fraction of the daily budget to invest. In this paper, we study the problem of automating the online joint bid/daily budget optimization of pay-per-click advertising campaigns over multiple channels. We formulate our problem as a combinatorial semi-bandit problem, which requires solving a special case of the Multiple-Choice Knapsack problem every day. Furthermore, for every campaign, we capture the dependency of the number of clicks on the bid and daily budget by Gaussian Processes, thus requiring mild assumptions on the regularity of these functions. We design four algorithms and show that they suffer from a regret that is upper bounded with high probability as O(sqrt{T}), where T is the time horizon of the learning process. We experimentally evaluate our algorithms with synthetic settings generated from real data from Yahoo!, and we present the results of the adoption of our algorithms in a real-world application with a daily average spent of 1,000 Euros for more than one year.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge