Online Joint Bid/Daily Budget Optimization of Internet Advertising Campaigns
Paper and Code
Mar 03, 2020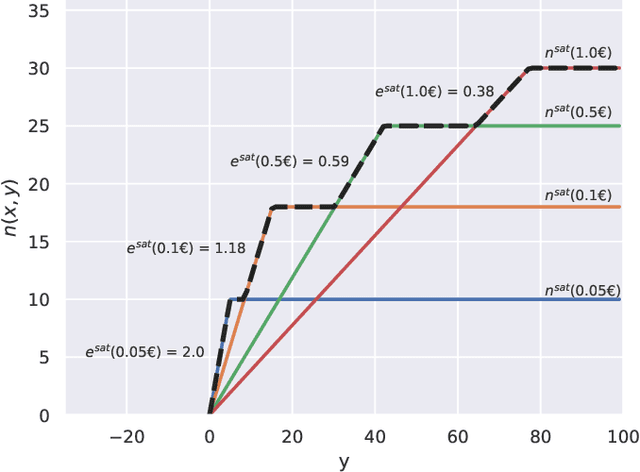
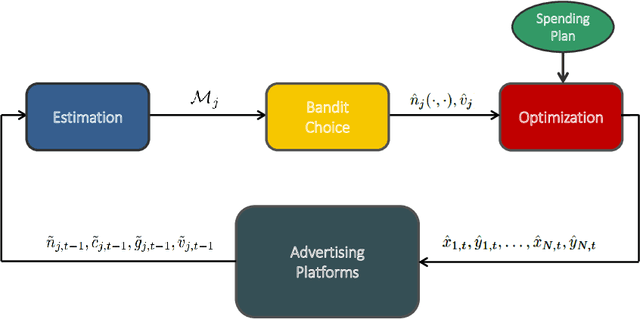
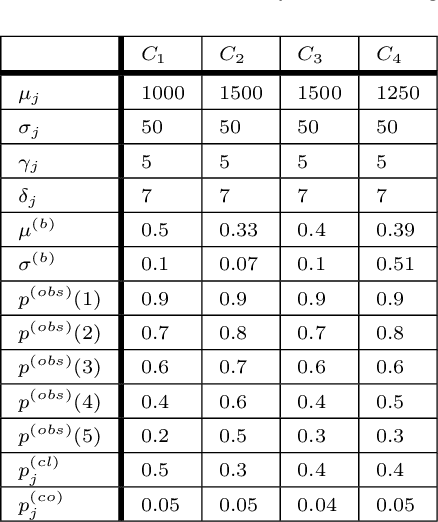
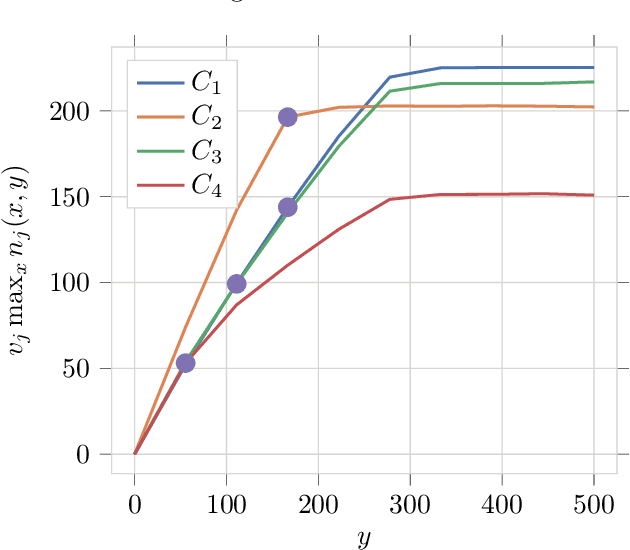
Pay-per-click advertising includes various formats (\emph{e.g.}, search, contextual, social) with a total investment of more than 200 billion USD per year worldwide. An advertiser is given a daily budget to allocate over several, even thousands, campaigns, mainly distinguishing for the ad, target, or channel. Furthermore, publishers choose the ads to display and how to allocate them employing auctioning mechanisms, in which every day the advertisers set for each campaign a bid corresponding to the maximum amount of money per click they are willing to pay and the fraction of the daily budget to invest. In this paper, we study the problem of automating the online joint bid/daily budget optimization of pay-per-click advertising campaigns over multiple channels. We formulate our problem as a combinatorial semi-bandit problem, which requires solving a special case of the Multiple-Choice Knapsack problem every day. Furthermore, for every campaign, we capture the dependency of the number of clicks on the bid and daily budget by Gaussian Processes, thus requiring mild assumptions on the regularity of these functions. We design four algorithms and show that they suffer from a regret that is upper bounded with high probability as O(sqrt{T}), where T is the time horizon of the learning process. We experimentally evaluate our algorithms with synthetic settings generated from real data from Yahoo!, and we present the results of the adoption of our algorithms in a real-world application with a daily average spent of 1,000 Euros for more than one year.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge