Davide Maran
A parametric algorithm is optimal for non-parametric regression of smooth functions
Dec 19, 2024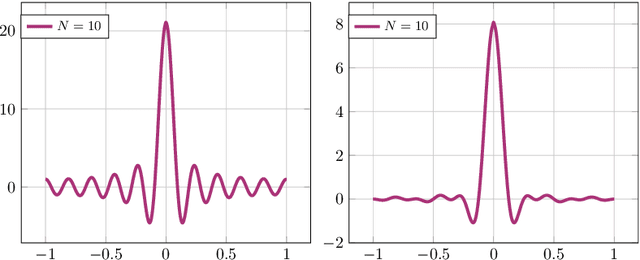

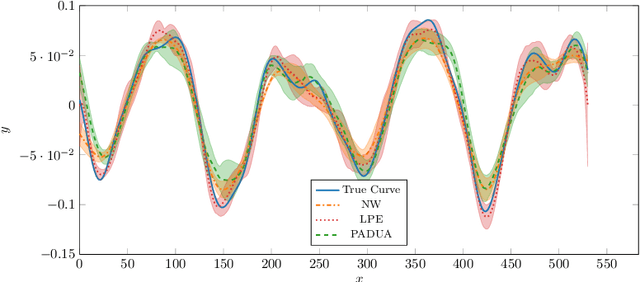
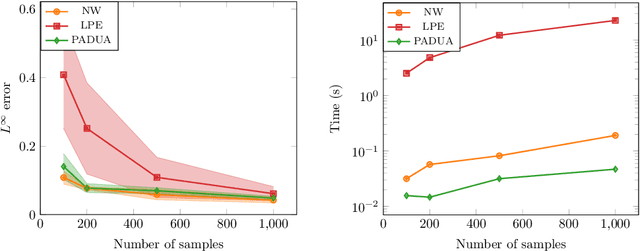
Abstract:We address the regression problem for a general function $f:[-1,1]^d\to \mathbb R$ when the learner selects the training points $\{x_i\}_{i=1}^n$ to achieve a uniform error bound across the entire domain. In this setting, known historically as nonparametric regression, we aim to establish a sample complexity bound that depends solely on the function's degree of smoothness. Assuming periodicity at the domain boundaries, we introduce PADUA, an algorithm that, with high probability, provides performance guarantees optimal up to constant or logarithmic factors across all problem parameters. Notably, PADUA is the first parametric algorithm with optimal sample complexity for this setting. Due to this feature, we prove that, differently from the non-parametric state of the art, PADUA enjoys optimal space complexity in the prediction phase. To validate these results, we perform numerical experiments over functions coming from real audio data, where PADUA shows comparable performance to state-of-the-art methods, while requiring only a fraction of the computational time.
Local Linearity: the Key for No-regret Reinforcement Learning in Continuous MDPs
Oct 31, 2024Abstract:Achieving the no-regret property for Reinforcement Learning (RL) problems in continuous state and action-space environments is one of the major open problems in the field. Existing solutions either work under very specific assumptions or achieve bounds that are vacuous in some regimes. Furthermore, many structural assumptions are known to suffer from a provably unavoidable exponential dependence on the time horizon $H$ in the regret, which makes any possible solution unfeasible in practice. In this paper, we identify local linearity as the feature that makes Markov Decision Processes (MDPs) both learnable (sublinear regret) and feasible (regret that is polynomial in $H$). We define a novel MDP representation class, namely Locally Linearizable MDPs, generalizing other representation classes like Linear MDPs and MDPS with low inherent Belmman error. Then, i) we introduce Cinderella, a no-regret algorithm for this general representation class, and ii) we show that all known learnable and feasible MDP families are representable in this class. We first show that all known feasible MDPs belong to a family that we call Mildly Smooth MDPs. Then, we show how any mildly smooth MDP can be represented as a Locally Linearizable MDP by an appropriate choice of representation. This way, Cinderella is shown to achieve state-of-the-art regret bounds for all previously known (and some new) continuous MDPs for which RL is learnable and feasible.
Projection by Convolution: Optimal Sample Complexity for Reinforcement Learning in Continuous-Space MDPs
May 10, 2024Abstract:We consider the problem of learning an $\varepsilon$-optimal policy in a general class of continuous-space Markov decision processes (MDPs) having smooth Bellman operators. Given access to a generative model, we achieve rate-optimal sample complexity by performing a simple, \emph{perturbed} version of least-squares value iteration with orthogonal trigonometric polynomials as features. Key to our solution is a novel projection technique based on ideas from harmonic analysis. Our~$\widetilde{\mathcal{O}}(\epsilon^{-2-d/(\nu+1)})$ sample complexity, where $d$ is the dimension of the state-action space and $\nu$ the order of smoothness, recovers the state-of-the-art result of discretization approaches for the special case of Lipschitz MDPs $(\nu=0)$. At the same time, for $\nu\to\infty$, it recovers and greatly generalizes the $\mathcal{O}(\epsilon^{-2})$ rate of low-rank MDPs, which are more amenable to regression approaches. In this sense, our result bridges the gap between two popular but conflicting perspectives on continuous-space MDPs.
No-Regret Reinforcement Learning in Smooth MDPs
Feb 06, 2024Abstract:Obtaining no-regret guarantees for reinforcement learning (RL) in the case of problems with continuous state and/or action spaces is still one of the major open challenges in the field. Recently, a variety of solutions have been proposed, but besides very specific settings, the general problem remains unsolved. In this paper, we introduce a novel structural assumption on the Markov decision processes (MDPs), namely $\nu-$smoothness, that generalizes most of the settings proposed so far (e.g., linear MDPs and Lipschitz MDPs). To face this challenging scenario, we propose two algorithms for regret minimization in $\nu-$smooth MDPs. Both algorithms build upon the idea of constructing an MDP representation through an orthogonal feature map based on Legendre polynomials. The first algorithm, \textsc{Legendre-Eleanor}, archives the no-regret property under weaker assumptions but is computationally inefficient, whereas the second one, \textsc{Legendre-LSVI}, runs in polynomial time, although for a smaller class of problems. After analyzing their regret properties, we compare our results with state-of-the-art ones from RL theory, showing that our algorithms achieve the best guarantees.
Autoregressive Bandits
Dec 12, 2022Abstract:Autoregressive processes naturally arise in a large variety of real-world scenarios, including e.g., stock markets, sell forecasting, weather prediction, advertising, and pricing. When addressing a sequential decision-making problem in such a context, the temporal dependence between consecutive observations should be properly accounted for converge to the optimal decision policy. In this work, we propose a novel online learning setting, named Autoregressive Bandits (ARBs), in which the observed reward follows an autoregressive process of order $k$, whose parameters depend on the action the agent chooses, within a finite set of $n$ actions. Then, we devise an optimistic regret minimization algorithm AutoRegressive Upper Confidence Bounds (AR-UCB) that suffers regret of order $\widetilde{\mathcal{O}} \left( \frac{(k+1)^{3/2}\sqrt{nT}}{(1-\Gamma)^2} \right)$, being $T$ the optimization horizon and $\Gamma < 1$ an index of the stability of the system. Finally, we present a numerical validation in several synthetic and one real-world setting, in comparison with general and specific purpose bandit baselines showing the advantages of the proposed approach.
Tight Performance Guarantees of Imitator Policies with Continuous Actions
Dec 07, 2022Abstract:Behavioral Cloning (BC) aims at learning a policy that mimics the behavior demonstrated by an expert. The current theoretical understanding of BC is limited to the case of finite actions. In this paper, we study BC with the goal of providing theoretical guarantees on the performance of the imitator policy in the case of continuous actions. We start by deriving a novel bound on the performance gap based on Wasserstein distance, applicable for continuous-action experts, holding under the assumption that the value function is Lipschitz continuous. Since this latter condition is hardy fulfilled in practice, even for Lipschitz Markov Decision Processes and policies, we propose a relaxed setting, proving that value function is always Holder continuous. This result is of independent interest and allows obtaining in BC a general bound for the performance of the imitator policy. Finally, we analyze noise injection, a common practice in which the expert action is executed in the environment after the application of a noise kernel. We show that this practice allows deriving stronger performance guarantees, at the price of a bias due to the noise addition.
Delayed Reinforcement Learning by Imitation
May 11, 2022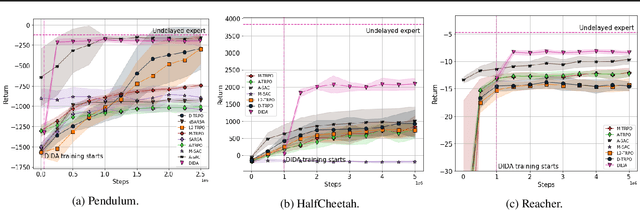

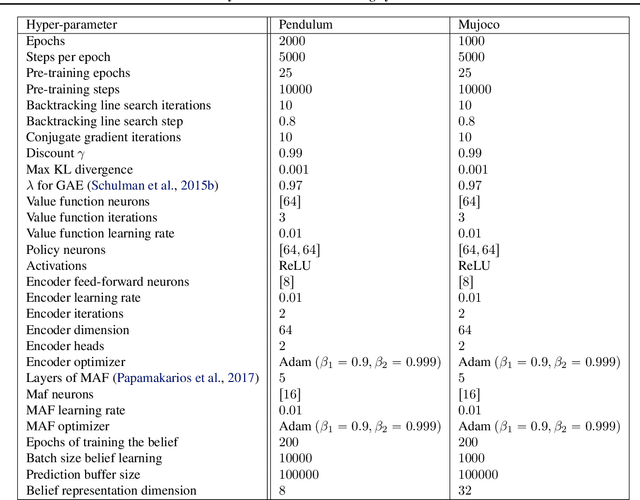
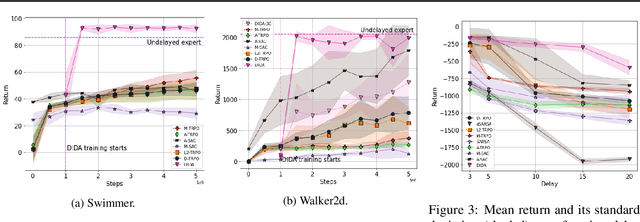
Abstract:When the agent's observations or interactions are delayed, classic reinforcement learning tools usually fail. In this paper, we propose a simple yet new and efficient solution to this problem. We assume that, in the undelayed environment, an efficient policy is known or can be easily learned, but the task may suffer from delays in practice and we thus want to take them into account. We present a novel algorithm, Delayed Imitation with Dataset Aggregation (DIDA), which builds upon imitation learning methods to learn how to act in a delayed environment from undelayed demonstrations. We provide a theoretical analysis of the approach that will guide the practical design of DIDA. These results are also of general interest in the delayed reinforcement learning literature by providing bounds on the performance between delayed and undelayed tasks, under smoothness conditions. We show empirically that DIDA obtains high performances with a remarkable sample efficiency on a variety of tasks, including robotic locomotion, classic control, and trading.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge