Physics-Aware Multifidelity Bayesian Optimization: a Generalized Formulation

The adoption of high-fidelity models for many-query optimization problems is majorly limited by the significant computational cost required for their evaluation at every query. Multifidelity Bayesian methods (MFBO) allow to include costly high-fidelity responses for a sub-selection of queries only, and use fast lower-fidelity models to accelerate the optimization process. State-of-the-art methods rely on a purely data-driven search and do not include explicit information about the physical context. This paper acknowledges that prior knowledge about the physical domains of engineering problems can be leveraged to accelerate these data-driven searches, and proposes a generalized formulation for MFBO to embed a form of domain awareness during the optimization procedure. In particular, we formalize a bias as a multifidelity acquisition function that captures the physical structure of the domain. This permits to partially alleviate the data-driven search from learning the domain properties on-the-fly, and sensitively enhances the management of multiple sources of information. The method allows to efficiently include high-fidelity simulations to guide the optimization search while containing the overall computational expense. Our physics-aware multifidelity Bayesian optimization is presented and illustrated for two classes of optimization problems frequently met in science and engineering, namely design optimization and health monitoring problems.

Active Learning and Bayesian Optimization: a Unified Perspective to Learn with a Goal

Both Bayesian optimization and active learning realize an adaptive sampling scheme to achieve a specific learning goal. However, while the two fields have seen an exponential growth in popularity in the past decade, their dualism has received relatively little attention. In this paper, we argue for an original unified perspective of Bayesian optimization and active learning based on the synergy between the principles driving the sampling policies. This symbiotic relationship is demonstrated through the substantial analogy between the infill criteria of Bayesian optimization and the learning criteria in active learning, and is formalized for the case of single information source and when multiple sources at different levels of fidelity are available. We further investigate the capabilities of each infill criteria both individually and in combination on a variety of analytical benchmark problems, to highlight benefits and limitations over mathematical properties that characterize real-world applications.

Non-Myopic Multifidelity Bayesian Optimization

Bayesian optimization is a popular framework for the optimization of black box functions. Multifidelity methods allows to accelerate Bayesian optimization by exploiting low-fidelity representations of expensive objective functions. Popular multifidelity Bayesian strategies rely on sampling policies that account for the immediate reward obtained evaluating the objective function at a specific input, precluding greater informative gains that might be obtained looking ahead more steps. This paper proposes a non-myopic multifidelity Bayesian framework to grasp the long-term reward from future steps of the optimization. Our computational strategy comes with a two-step lookahead multifidelity acquisition function that maximizes the cumulative reward obtained measuring the improvement in the solution over two steps ahead. We demonstrate that the proposed algorithm outperforms a standard multifidelity Bayesian framework on popular benchmark optimization problems.

Computational framework for real-time diagnostics and prognostics of aircraft actuation systems

Prognostics and Health Management (PHM) are emerging approaches to product life cycle that will maintain system safety and improve reliability, while reducing operating and maintenance costs. This is particularly relevant for aerospace systems, where high levels of integrity and high performances are required at the same time. We propose a novel strategy for the nearly real-time Fault Detection and Identification (FDI) of a dynamical assembly, and for the estimation of Remaining Useful Life (RUL) of the system. The availability of a timely estimate of the health status of the system will allow for an informed adaptive planning of maintenance and a dynamical reconfiguration of the mission profile, reducing operating costs and improving reliability. This work addresses the three phases of the prognostic flow - namely (1) signal acquisition, (2) Fault Detection and Identification, and (3) Remaining Useful Life estimation - and introduces a computationally efficient procedure suitable for real-time, on-board execution. To achieve this goal, we propose to combine information from physical models of different fidelity with machine learning techniques to obtain efficient representations (surrogate models) suitable for nearly real-time applications. Additionally, we propose an importance sampling strategy and a novel approach to model damage propagation for dynamical systems. The methodology is assessed for the FDI and RUL estimation of an aircraft electromechanical actuator (EMA) for secondary flight controls. The results show that the proposed method allows for a high precision in the evaluation of the system RUL, while outperforming common model-based techniques in terms of computational time.

Resource Aware Multifidelity Active Learning for Efficient Optimization

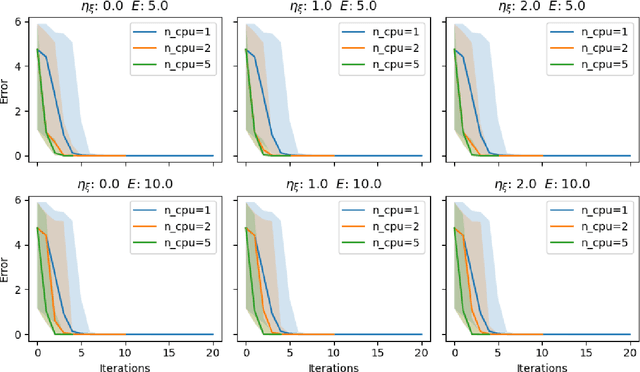
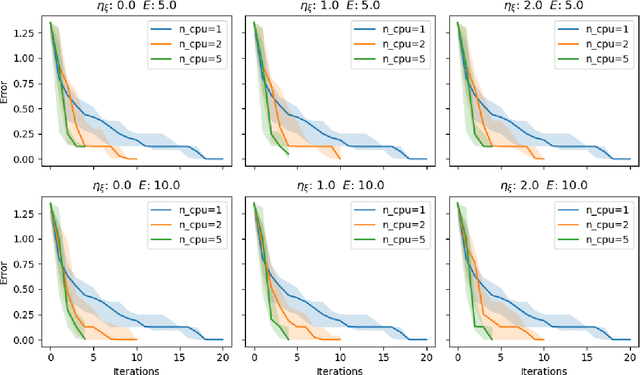
Traditional methods for black box optimization require a considerable number of evaluations which can be time consuming, unpractical, and often unfeasible for many engineering applications that rely on accurate representations and expensive models to evaluate. Bayesian Optimization (BO) methods search for the global optimum by progressively (actively) learning a surrogate model of the objective function along the search path. Bayesian optimization can be accelerated through multifidelity approaches which leverage multiple black-box approximations of the objective functions that can be computationally cheaper to evaluate, but still provide relevant information to the search task. Further computational benefits are offered by the availability of parallel and distributed computing architectures whose optimal usage is an open opportunity within the context of active learning. This paper introduces the Resource Aware Active Learning (RAAL) strategy, a multifidelity Bayesian scheme to accelerate the optimization of black box functions. At each optimization step, the RAAL procedure computes the set of best sample locations and the associated fidelity sources that maximize the information gain to acquire during the parallel/distributed evaluation of the objective function, while accounting for the limited computational budget. The scheme is demonstrated for a variety of benchmark problems and results are discussed for both single fidelity and multifidelity settings. In particular we observe that the RAAL strategy optimally seeds multiple points at each iteration allowing for a major speed up of the optimization task.