Some limitations of norm based generalization bounds in deep neural networks
Paper and Code
May 23, 2019
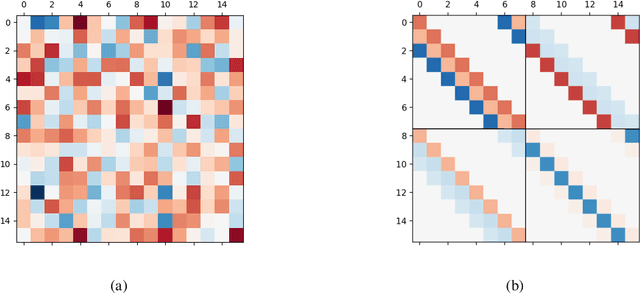

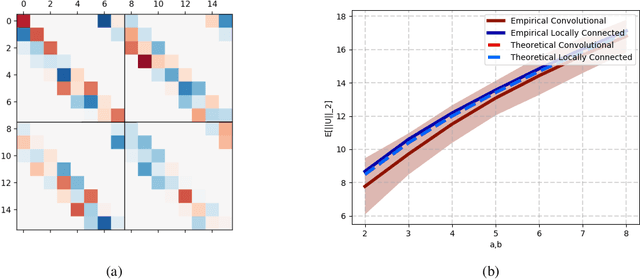
Deep convolutional neural networks have been shown to be able to fit a labeling over random data while still being able to generalize well on normal datasets. Describing deep convolutional neural network capacity through the measure of spectral complexity has been recently proposed to tackle this apparent paradox. Spectral complexity correlates with GE and can distinguish networks trained on normal and random labels. We propose the first GE bound based on spectral complexity for deep convolutional neural networks and provide tighter bounds by orders of magnitude from the previous estimate. We then investigate theoretically and empirically the insensitivity of spectral complexity to invariances of modern deep convolutional neural networks, and show several limitations of spectral complexity that occur as a result.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge