Revisiting hard thresholding for DNN pruning

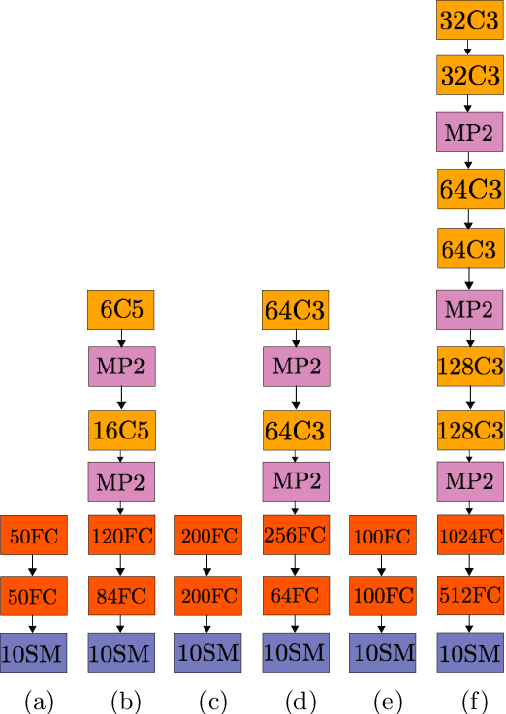
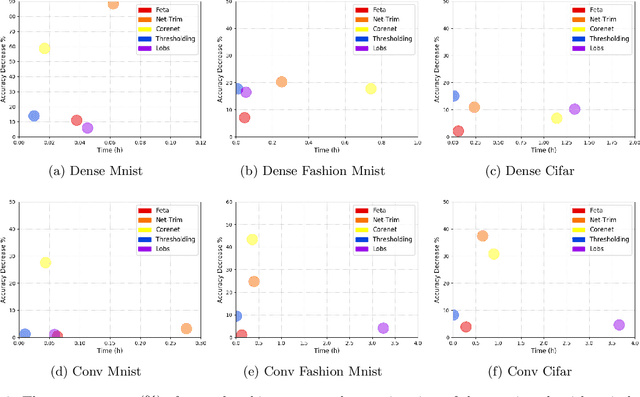
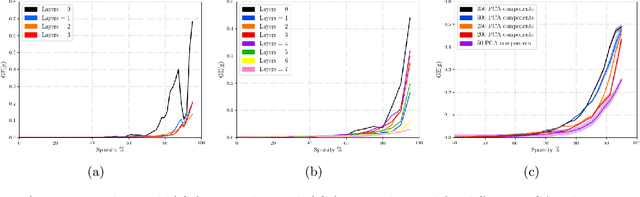
The most common method for DNN pruning is hard thresholding of network weights, followed by retraining to recover any lost accuracy. Recently developed smart pruning algorithms use the DNN response over the training set for a variety of cost functions to determine redundant network weights, leading to less accuracy degradation and possibly less retraining time. For experiments on the total pruning time (pruning time + retraining time) we show that hard thresholding followed by retraining remains the most efficient way of reducing the number of network parameters. However smart pruning algorithms still have advantages when retraining is not possible. In this context we propose a novel smart pruning algorithm based on difference of convex functions optimisation and show that it is often orders of magnitude faster than competing approaches while achieving the lowest classification accuracy degradation. Furthermore we investigate theoretically the effect of hard thresholding on DNN accuracy. We show that accuracy degradation increases with remaining network depth from the pruned layer. We also discover a link between the latent dimensionality of the training data manifold and network robustness to hard thresholding.