FairJob: A Real-World Dataset for Fairness in Online Systems

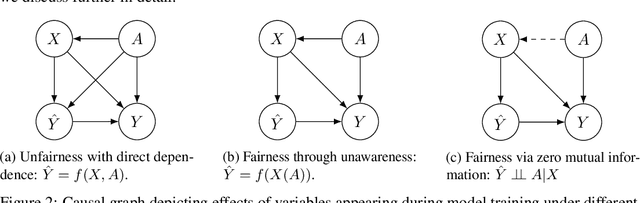
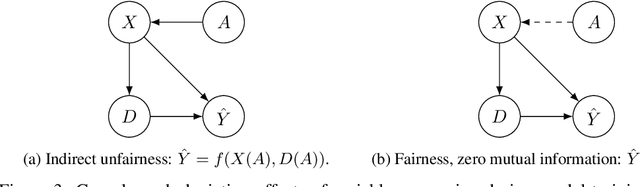
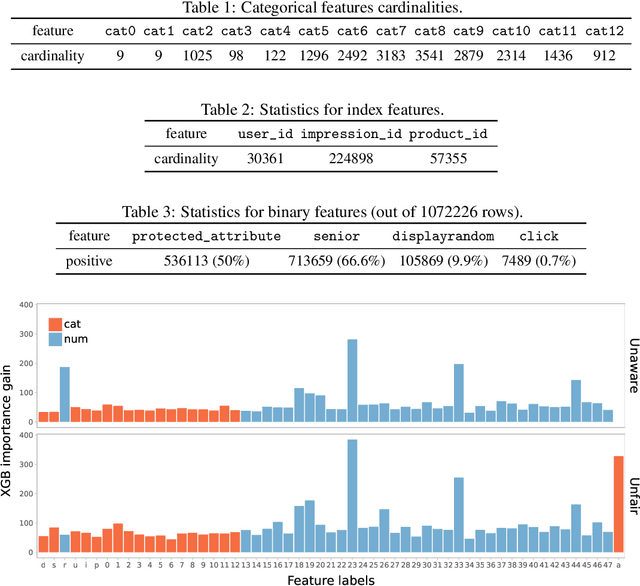
We introduce a fairness-aware dataset for job recommendation in advertising, designed to foster research in algorithmic fairness within real-world scenarios. It was collected and prepared to comply with privacy standards and business confidentiality. An additional challenge is the lack of access to protected user attributes such as gender, for which we propose a solution to obtain a proxy estimate. Despite being anonymized and including a proxy for a sensitive attribute, our dataset preserves predictive power and maintains a realistic and challenging benchmark. This dataset addresses a significant gap in the availability of fairness-focused resources for high-impact domains like advertising -- the actual impact being having access or not to precious employment opportunities, where balancing fairness and utility is a common industrial challenge. We also explore various stages in the advertising process where unfairness can occur and introduce a method to compute a fair utility metric for the job recommendations in online systems case from a biased dataset. Experimental evaluations of bias mitigation techniques on the released dataset demonstrate potential improvements in fairness and the associated trade-offs with utility.

Maximizing the Success Probability of Policy Allocations in Online Systems

The effectiveness of advertising in e-commerce largely depends on the ability of merchants to bid on and win impressions for their targeted users. The bidding procedure is highly complex due to various factors such as market competition, user behavior, and the diverse objectives of advertisers. In this paper we consider the problem at the level of user timelines instead of individual bid requests, manipulating full policies (i.e. pre-defined bidding strategies) and not bid values. In order to optimally allocate policies to users, typical multiple treatments allocation methods solve knapsack-like problems which aim at maximizing an expected value under constraints. In the industrial contexts such as online advertising, we argue that optimizing for the probability of success is a more suited objective than expected value maximization, and we introduce the SuccessProbaMax algorithm that aims at finding the policy allocation which is the most likely to outperform a fixed reference policy. Finally, we conduct comprehensive experiments both on synthetic and real-world data to evaluate its performance. The results demonstrate that our proposed algorithm outperforms conventional expected-value maximization algorithms in terms of success rate.

A Primer on Bayesian Neural Networks: Review and Debates

Neural networks have achieved remarkable performance across various problem domains, but their widespread applicability is hindered by inherent limitations such as overconfidence in predictions, lack of interpretability, and vulnerability to adversarial attacks. To address these challenges, Bayesian neural networks (BNNs) have emerged as a compelling extension of conventional neural networks, integrating uncertainty estimation into their predictive capabilities. This comprehensive primer presents a systematic introduction to the fundamental concepts of neural networks and Bayesian inference, elucidating their synergistic integration for the development of BNNs. The target audience comprises statisticians with a potential background in Bayesian methods but lacking deep learning expertise, as well as machine learners proficient in deep neural networks but with limited exposure to Bayesian statistics. We provide an overview of commonly employed priors, examining their impact on model behavior and performance. Additionally, we delve into the practical considerations associated with training and inference in BNNs. Furthermore, we explore advanced topics within the realm of BNN research, acknowledging the existence of ongoing debates and controversies. By offering insights into cutting-edge developments, this primer not only equips researchers and practitioners with a solid foundation in BNNs, but also illuminates the potential applications of this dynamic field. As a valuable resource, it fosters an understanding of BNNs and their promising prospects, facilitating further advancements in the pursuit of knowledge and innovation.

Dependence between Bayesian neural network units

The connection between Bayesian neural networks and Gaussian processes gained a lot of attention in the last few years, with the flagship result that hidden units converge to a Gaussian process limit when the layers width tends to infinity. Underpinning this result is the fact that hidden units become independent in the infinite-width limit. Our aim is to shed some light on hidden units dependence properties in practical finite-width Bayesian neural networks. In addition to theoretical results, we assess empirically the depth and width impacts on hidden units dependence properties.

Bayesian neural network unit priors and generalized Weibull-tail property

The connection between Bayesian neural networks and Gaussian processes gained a lot of attention in the last few years. Hidden units are proven to follow a Gaussian process limit when the layer width tends to infinity. Recent work has suggested that finite Bayesian neural networks may outperform their infinite counterparts because they adapt their internal representations flexibly. To establish solid ground for future research on finite-width neural networks, our goal is to study the prior induced on hidden units. Our main result is an accurate description of hidden units tails which shows that unit priors become heavier-tailed going deeper, thanks to the introduced notion of generalized Weibull-tail. This finding sheds light on the behavior of hidden units of finite Bayesian neural networks.

Bayesian neural networks increasingly sparsify their units with depth

We investigate deep Bayesian neural networks with Gaussian priors on the weights and ReLU-like nonlinearities, shedding light on novel sparsity-inducing mechanisms at the level of the units of the network, both pre- and post-nonlinearities. The main thrust of the paper is to establish that the units prior distribution becomes increasingly heavy-tailed with depth. We show that first layer units are Gaussian, second layer units are sub-Exponential, and we introduce sub-Weibull distributions to characterize the deeper layers units. Bayesian neural networks with Gaussian priors are well known to induce the weight decay penalty on the weights. In contrast, our result indicates a more elaborate regularisation scheme at the level of the units, ranging from convex penalties for the first two layers - weight decay for the first and Lasso for the second - to non convex penalties for deeper layers. Thus, despite weight decay does not allow for the weights to be set exactly to zero, sparse solutions tend to be selected for the units from the second layer onward. This result provides new theoretical insight on deep Bayesian neural networks, underpinning their natural shrinkage properties and practical potential.