Better PAC-Bayes Bounds for Deep Neural Networks using the Loss Curvature

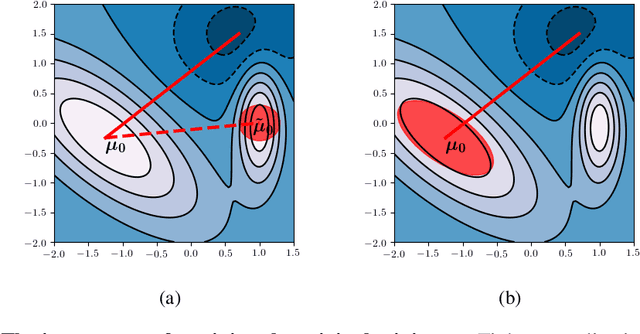
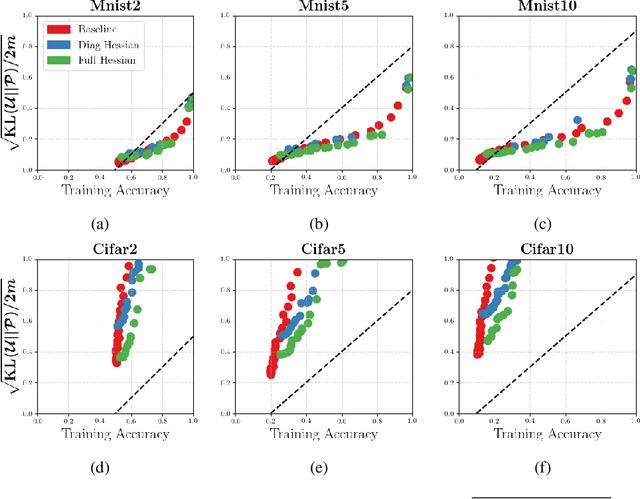
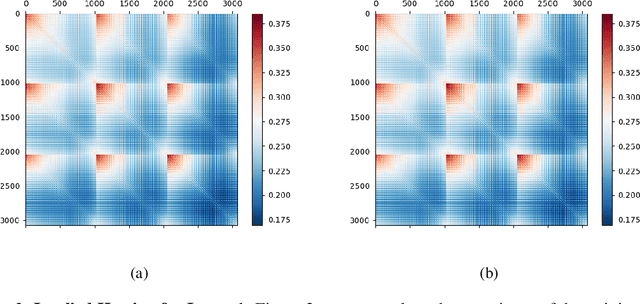
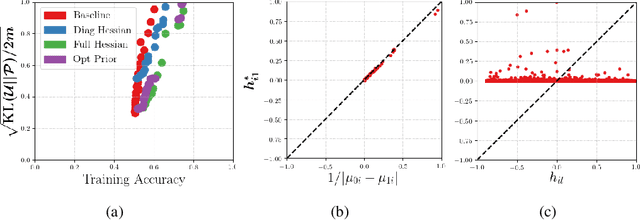
We investigate whether it's possible to tighten PAC-Bayes bounds for deep neural networks by utilizing the Hessian of the training loss at the minimum. For the case of Gaussian priors and posteriors we introduce a Hessian-based method to obtain tighter PAC-Bayes bounds that relies on closed form solutions of layerwise subproblems. We thus avoid commonly used variational inference techniques which can be difficult to implement and time consuming for modern deep architectures. Through careful experiments we analyze the influence of the prior mean, prior covariance, posterior mean and posterior covariance on obtaining tighter bounds. We discuss several limitations in further improving PAC-Bayes bounds through more informative priors.