Pierre Wolinski
Adapting Newton's Method to Neural Networks through a Summary of Higher-Order Derivatives
Dec 06, 2023Abstract:We consider a gradient-based optimization method applied to a function $\mathcal{L}$ of a vector of variables $\boldsymbol{\theta}$, in the case where $\boldsymbol{\theta}$ is represented as a tuple of tensors $(\mathbf{T}_1, \cdots, \mathbf{T}_S)$. This framework encompasses many common use-cases, such as training neural networks by gradient descent. First, we propose a computationally inexpensive technique providing higher-order information on $\mathcal{L}$, especially about the interactions between the tensors $\mathbf{T}_s$, based on automatic differentiation and computational tricks. Second, we use this technique at order 2 to build a second-order optimization method which is suitable, among other things, for training deep neural networks of various architectures. This second-order method leverages the partition structure of $\boldsymbol{\theta}$ into tensors $(\mathbf{T}_1, \cdots, \mathbf{T}_S)$, in such a way that it requires neither the computation of the Hessian of $\mathcal{L}$ according to $\boldsymbol{\theta}$, nor any approximation of it. The key part consists in computing a smaller matrix interpretable as a "Hessian according to the partition", which can be computed exactly and efficiently. In contrast to many existing practical second-order methods used in neural networks, which perform a diagonal or block-diagonal approximation of the Hessian or its inverse, the method we propose does not neglect interactions between layers. Finally, we can tune the coarseness of the partition to recover well-known optimization methods: the coarsest case corresponds to Cauchy's steepest descent method, the finest case corresponds to the usual Newton's method.
Efficient Neural Networks for Tiny Machine Learning: A Comprehensive Review
Nov 20, 2023Abstract:The field of Tiny Machine Learning (TinyML) has gained significant attention due to its potential to enable intelligent applications on resource-constrained devices. This review provides an in-depth analysis of the advancements in efficient neural networks and the deployment of deep learning models on ultra-low power microcontrollers (MCUs) for TinyML applications. It begins by introducing neural networks and discussing their architectures and resource requirements. It then explores MEMS-based applications on ultra-low power MCUs, highlighting their potential for enabling TinyML on resource-constrained devices. The core of the review centres on efficient neural networks for TinyML. It covers techniques such as model compression, quantization, and low-rank factorization, which optimize neural network architectures for minimal resource utilization on MCUs. The paper then delves into the deployment of deep learning models on ultra-low power MCUs, addressing challenges such as limited computational capabilities and memory resources. Techniques like model pruning, hardware acceleration, and algorithm-architecture co-design are discussed as strategies to enable efficient deployment. Lastly, the review provides an overview of current limitations in the field, including the trade-off between model complexity and resource constraints. Overall, this review paper presents a comprehensive analysis of efficient neural networks and deployment strategies for TinyML on ultra-low-power MCUs. It identifies future research directions for unlocking the full potential of TinyML applications on resource-constrained devices.
Imposing Gaussian Pre-Activations in a Neural Network
May 24, 2022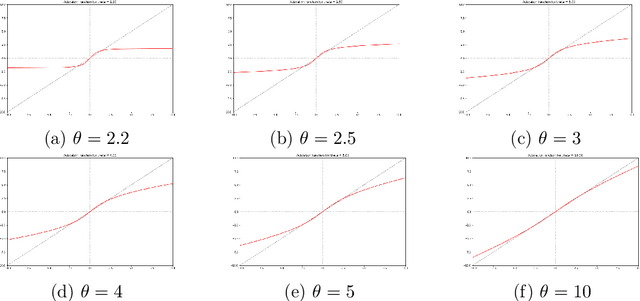
Abstract:The goal of the present work is to propose a way to modify both the initialization distribution of the weights of a neural network and its activation function, such that all pre-activations are Gaussian. We propose a family of pairs initialization/activation, where the activation functions span a continuum from bounded functions (such as Heaviside or tanh) to the identity function. This work is motivated by the contradiction between existing works dealing with Gaussian pre-activations: on one side, the works in the line of the Neural Tangent Kernels and the Edge of Chaos are assuming it, while on the other side, theoretical and experimental results challenge this hypothesis. The family of pairs initialization/activation we are proposing will help us to answer this hot question: is it desirable to have Gaussian pre-activations in a neural network?
Interpreting a Penalty as the Influence of a Bayesian Prior
Feb 01, 2020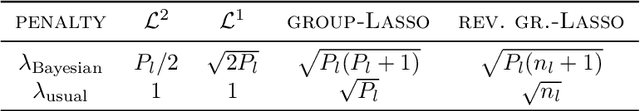
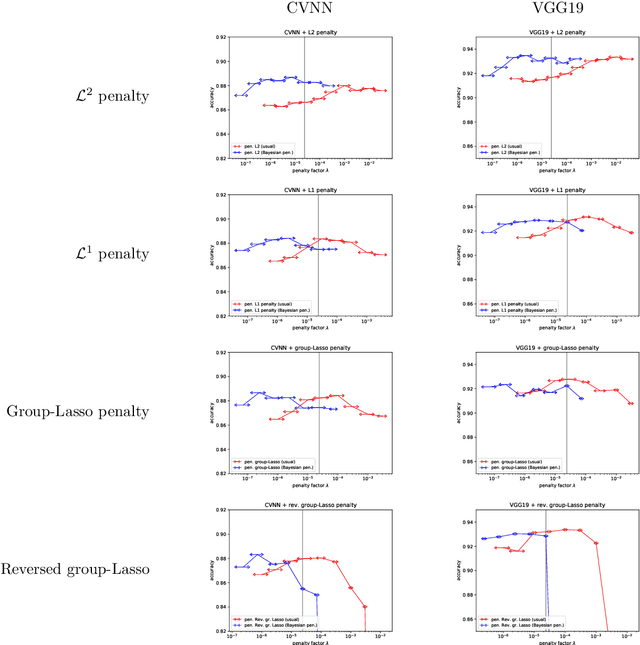

Abstract:In machine learning, it is common to optimize the parameters of a probabilistic model, modulated by a somewhat ad hoc regularization term that penalizes some values of the parameters. Regularization terms appear naturally in Variational Inference (VI), a tractable way to approximate Bayesian posteriors: the loss to optimize contains a Kullback--Leibler divergence term between the approximate posterior and a Bayesian prior. We fully characterize which regularizers can arise this way, and provide a systematic way to compute the corresponding prior. This viewpoint also provides a prediction for useful values of the regularization factor in neural networks. We apply this framework to regularizers such as L1 or group-Lasso.
Learning with Random Learning Rates
Oct 03, 2018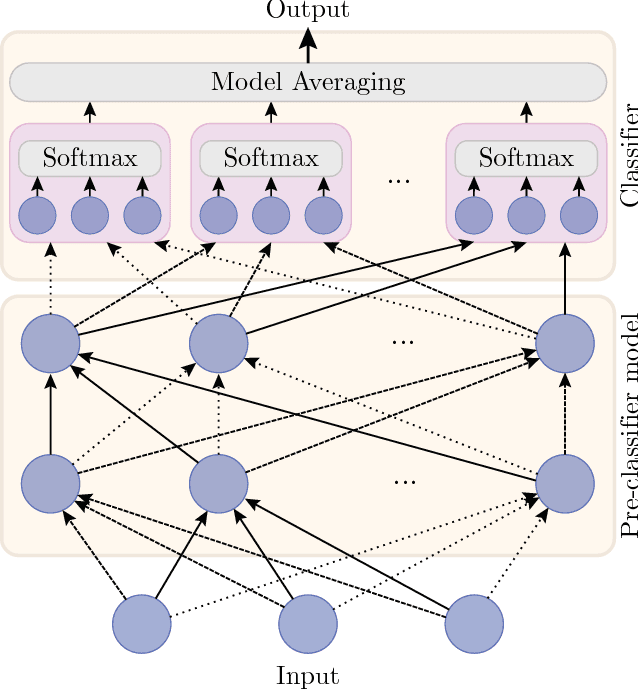
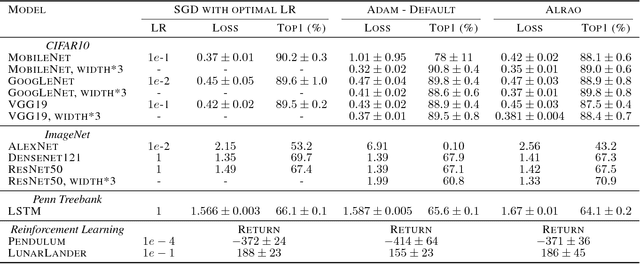
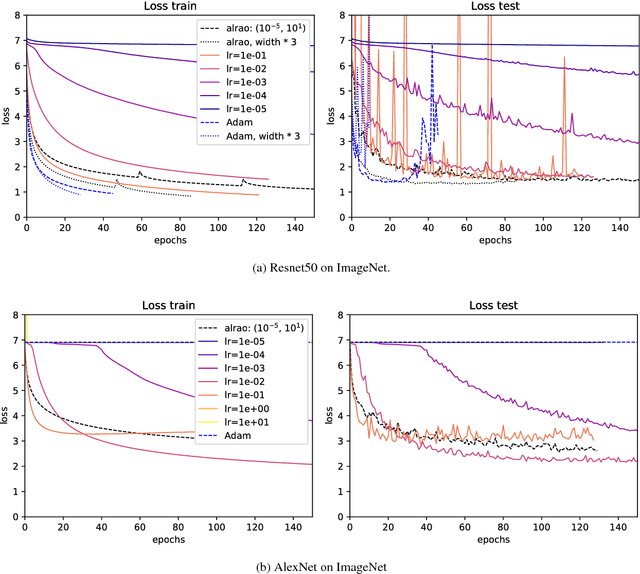
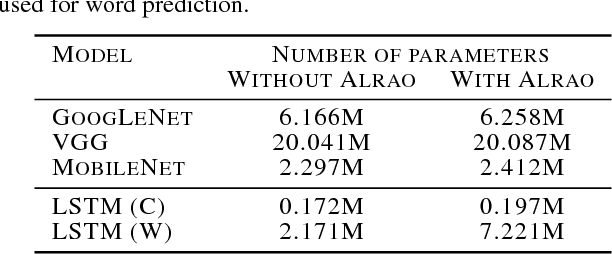
Abstract:Hyperparameter tuning is a bothersome step in the training of deep learning models. One of the most sensitive hyperparameters is the learning rate of the gradient descent. We present the 'All Learning Rates At Once' (Alrao) optimization method for neural networks: each unit or feature in the network gets its own learning rate sampled from a random distribution spanning several orders of magnitude. This comes at practically no computational cost. Perhaps surprisingly, stochastic gradient descent (SGD) with Alrao performs close to SGD with an optimally tuned learning rate, for various architectures and problems. Alrao could save time when testing deep learning models: a range of models could be quickly assessed with Alrao, and the most promising models could then be trained more extensively. This text comes with a PyTorch implementation of the method, which can be plugged on an existing PyTorch model: https://github.com/leonardblier/alrao .
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge