Multi-fidelity Machine Learning for Uncertainty Quantification and Optimization

In system analysis and design optimization, multiple computational models are typically available to represent a given physical system. These models can be broadly classified as high-fidelity models, which provide highly accurate predictions but require significant computational resources, and low-fidelity models, which are computationally efficient but less accurate. Multi-fidelity methods integrate high- and low-fidelity models to balance computational cost and predictive accuracy. This perspective paper provides an in-depth overview of the emerging field of machine learning-based multi-fidelity methods, with a particular emphasis on uncertainty quantification and optimization. For uncertainty quantification, a particular focus is on multi-fidelity graph neural networks, compared with multi-fidelity polynomial chaos expansion. For optimization, our emphasis is on multi-fidelity Bayesian optimization, offering a unified perspective on multi-fidelity priors and proposing an application strategy when the objective function is an integral or a weighted sum. We highlight the current state of the art, identify critical gaps in the literature, and outline key research opportunities in this evolving field.

Optimizing Posterior Samples for Bayesian Optimization via Rootfinding

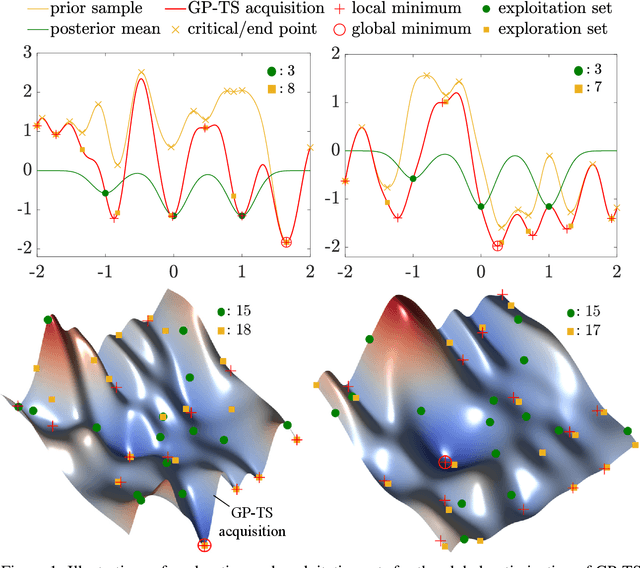
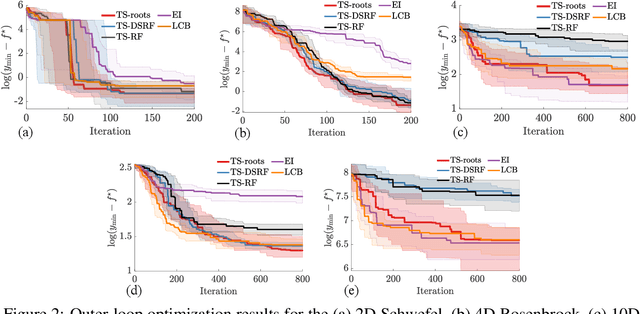
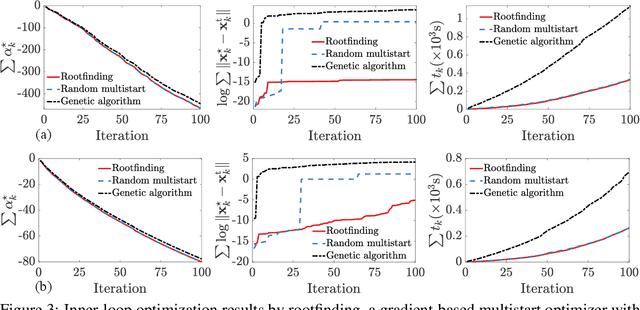
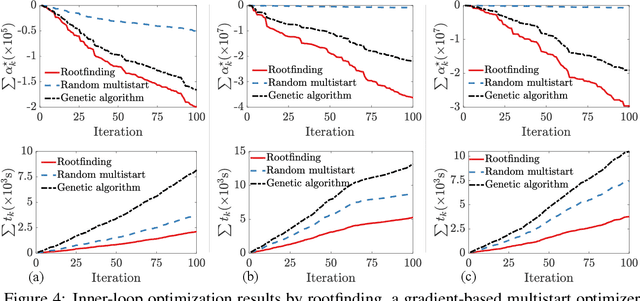
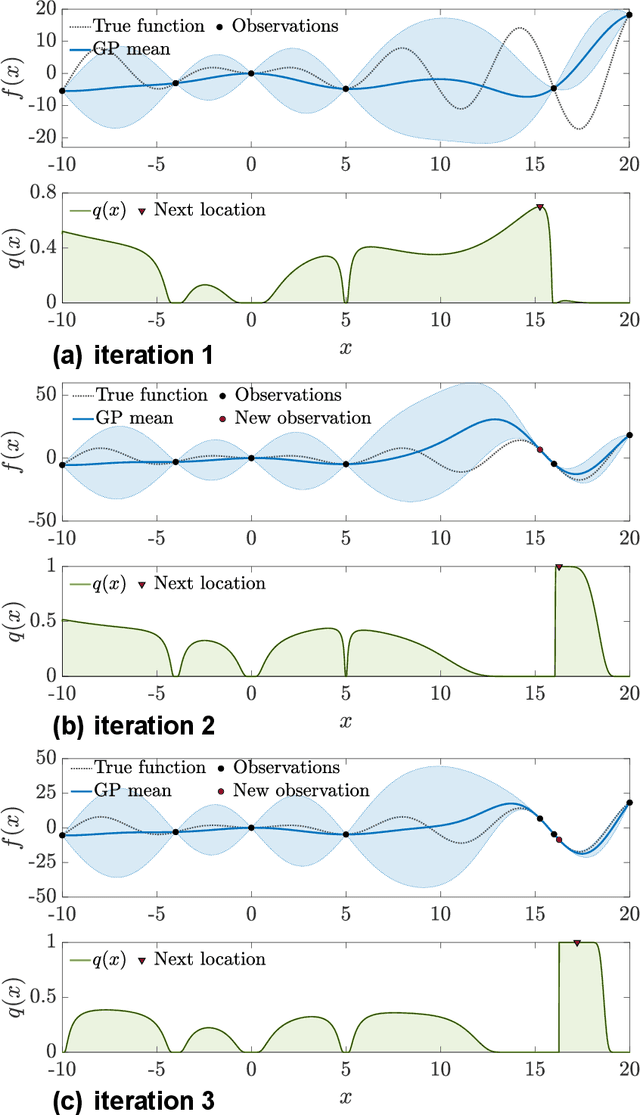
Bayesian optimization devolves the global optimization of a costly objective function to the global optimization of a sequence of acquisition functions. This inner-loop optimization can be catastrophically difficult if it involves posterior samples, especially in higher dimensions. We introduce an efficient global optimization strategy for posterior samples based on global rootfinding. It provides gradient-based optimizers with judiciously selected starting points, designed to combine exploitation and exploration. The algorithm scales practically linearly to high dimensions. For posterior sample-based acquisition functions such as Gaussian process Thompson sampling (GP-TS) and variants of entropy search, we demonstrate remarkable improvement in both inner- and outer-loop optimization, surprisingly outperforming alternatives like EI and GP-UCB in most cases. We also propose a sample-average formulation of GP-TS, which has a parameter to explicitly control exploitation and can be computed at the cost of one posterior sample. Our implementation is available at https://github.com/UQUH/TSRoots .

Gaussian Process Thompson Sampling via Rootfinding

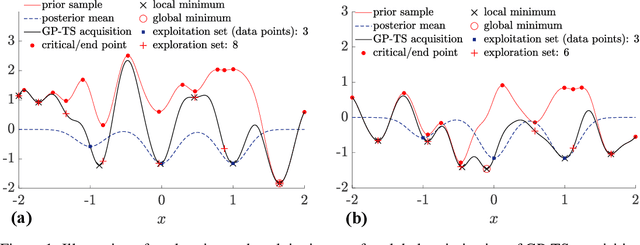
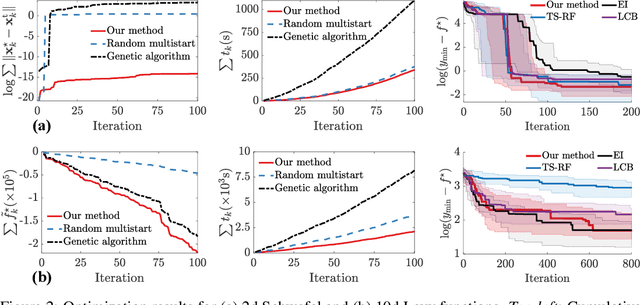
Thompson sampling (TS) is a simple, effective stochastic policy in Bayesian decision making. It samples the posterior belief about the reward profile and optimizes the sample to obtain a candidate decision. In continuous optimization, the posterior of the objective function is often a Gaussian process (GP), whose sample paths have numerous local optima, making their global optimization challenging. In this work, we introduce an efficient global optimization strategy for GP-TS that carefully selects starting points for gradient-based multi-start optimizers. It identifies all local optima of the prior sample via univariate global rootfinding, and optimizes the posterior sample using a differentiable, decoupled representation. We demonstrate remarkable improvement in the global optimization of GP posterior samples, especially in high dimensions. This leads to dramatic improvements in the overall performance of Bayesian optimization using GP-TS acquisition functions, surprisingly outperforming alternatives like GP-UCB and EI.

Automated design of nonreciprocal thermal emitters via Bayesian optimization

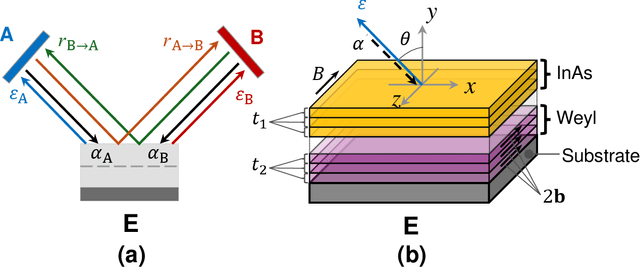
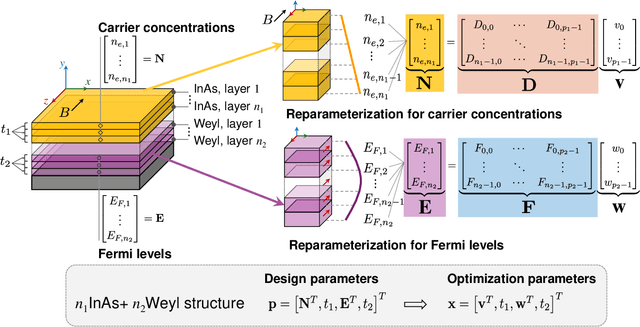
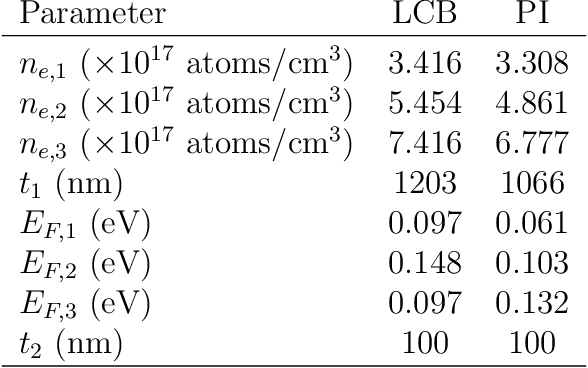
Nonreciprocal thermal emitters that break Kirchhoff's law of thermal radiation promise exciting applications for thermal and energy applications. The design of the bandwidth and angular range of the nonreciprocal effect, which directly affects the performance of nonreciprocal emitters, typically relies on physical intuition. In this study, we present a general numerical approach to maximize the nonreciprocal effect. We choose doped magneto-optic materials and magnetic Weyl semimetal materials as model materials and focus on pattern-free multilayer structures. The optimization randomly starts from a less effective structure and incrementally improves the broadband nonreciprocity through the combination of Bayesian optimization and reparameterization. Optimization results show that the proposed approach can discover structures that can achieve broadband nonreciprocal emission at wavelengths from 5 to 40 micrometers using only a fewer layers, significantly outperforming current state-of-the-art designs based on intuition in terms of both performance and simplicity.

Digital Twins and Civil Engineering Phases: Reorienting Adoption Strategies

Digital twin (DT) technology has received immense attention over the years due to the promises it presents to various stakeholders in science and engineering. As a result, different thematic areas of DT have been explored. This is no different in specific fields such as manufacturing, automation, oil and gas, and civil engineering, leading to fragmented approaches for field-specific applications. The civil engineering industry is further disadvantaged in this regard as it relies on external techniques by other engineering fields for its DT adoption. A rising consequence of these extensions is a concentrated application of DT to the operations and maintenance phase. On another spectrum, Building Information Modeling (BIM) are pervasively utilized in the planning/design phase, and the transient nature of the construction phase remains a challenge for its DT adoption. In this paper, we present a phase-based development of DT in the Architecture, Engineering, and Construction industry. We commence by presenting succinct expositions on DT as a concept and as a service and establish a five-level scale system. Furthermore, we present separately a systematic literature review of the conventional techniques employed at each civil engineering phase. In this regard, we identified enabling technologies such as computer vision for extended sensing and the Internet of Things for reliable integration. Ultimately, we attempt to reveal DT as an important tool across the entire life cycle of civil engineering projects and nudge researchers to think more holistically in their quest for the integration of DT for civil engineering applications.

Epsilon-Greedy Thompson Sampling to Bayesian Optimization

Thompson sampling (TS) serves as a solution for addressing the exploitation-exploration dilemma in Bayesian optimization (BO). While it prioritizes exploration by randomly generating and maximizing sample paths of Gaussian process (GP) posteriors, TS weakly manages its exploitation by gathering information about the true objective function after each exploration is performed. In this study, we incorporate the epsilon-greedy ($\varepsilon$-greedy) policy, a well-established selection strategy in reinforcement learning, into TS to improve its exploitation. We first delineate two extremes of TS applied for BO, namely the generic TS and a sample-average TS. The former and latter promote exploration and exploitation, respectively. We then use $\varepsilon$-greedy policy to randomly switch between the two extremes. A small value of $\varepsilon \in (0,1)$ prioritizes exploitation, and vice versa. We empirically show that $\varepsilon$-greedy TS with an appropriate $\varepsilon$ is better than one of its two extremes and competes with the other.

Multi-fidelity Bayesian Optimization in Engineering Design

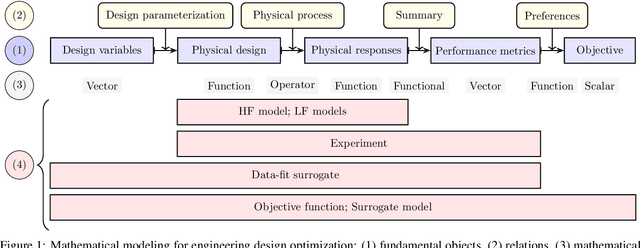
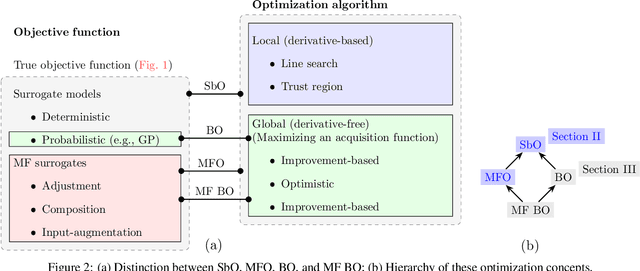
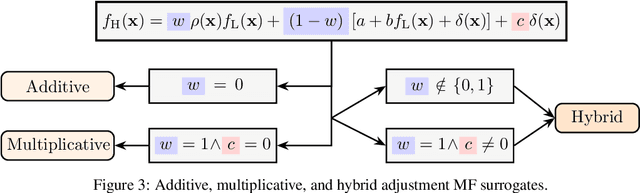
Resided at the intersection of multi-fidelity optimization (MFO) and Bayesian optimization (BO), MF BO has found a niche in solving expensive engineering design optimization problems, thanks to its advantages in incorporating physical and mathematical understandings of the problems, saving resources, addressing exploitation-exploration trade-off, considering uncertainty, and processing parallel computing. The increasing number of works dedicated to MF BO suggests the need for a comprehensive review of this advanced optimization technique. In this paper, we survey recent developments of two essential ingredients of MF BO: Gaussian process (GP) based MF surrogates and acquisition functions. We first categorize the existing MF modeling methods and MFO strategies to locate MF BO in a large family of surrogate-based optimization and MFO algorithms. We then exploit the common properties shared between the methods from each ingredient of MF BO to describe important GP-based MF surrogate models and review various acquisition functions. By doing so, we expect to provide a structured understanding of MF BO. Finally, we attempt to reveal important aspects that require further research for applications of MF BO in solving intricate yet important design optimization problems, including constrained optimization, high-dimensional optimization, optimization under uncertainty, and multi-objective optimization.

Gaussian Process Subspace Regression for Model Reduction

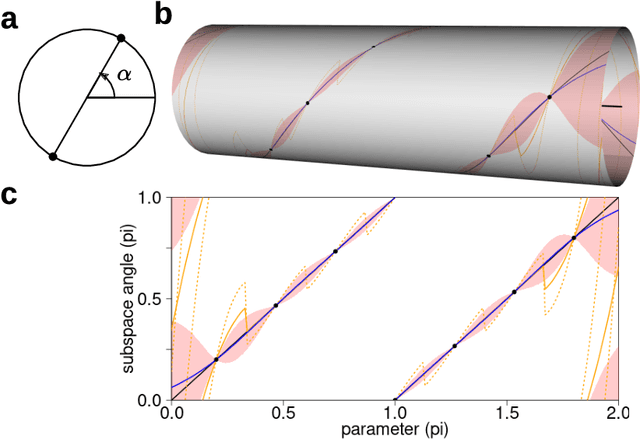
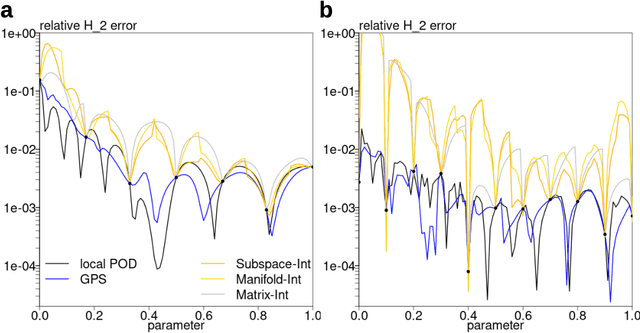
Subspace-valued functions arise in a wide range of problems, including parametric reduced order modeling (PROM). In PROM, each parameter point can be associated with a subspace, which is used for Petrov-Galerkin projections of large system matrices. Previous efforts to approximate such functions use interpolations on manifolds, which can be inaccurate and slow. To tackle this, we propose a novel Bayesian nonparametric model for subspace prediction: the Gaussian Process Subspace regression (GPS) model. This method is extrinsic and intrinsic at the same time: with multivariate Gaussian distributions on the Euclidean space, it induces a joint probability model on the Grassmann manifold, the set of fixed-dimensional subspaces. The GPS adopts a simple yet general correlation structure, and a principled approach for model selection. Its predictive distribution admits an analytical form, which allows for efficient subspace prediction over the parameter space. For PROM, the GPS provides a probabilistic prediction at a new parameter point that retains the accuracy of local reduced models, at a computational complexity that does not depend on system dimension, and thus is suitable for online computation. We give four numerical examples to compare our method to subspace interpolation, as well as two methods that interpolate local reduced models. Overall, GPS is the most data efficient, more computationally efficient than subspace interpolation, and gives smooth predictions with uncertainty quantification.

Normal-bundle Bootstrap

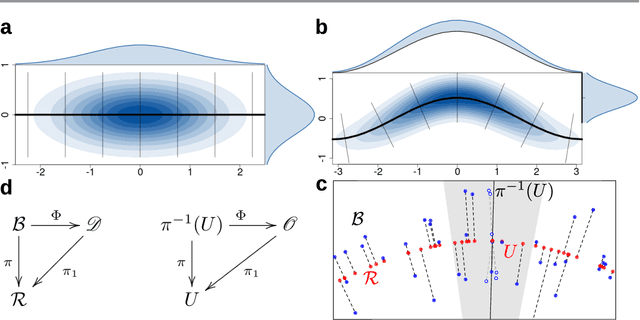
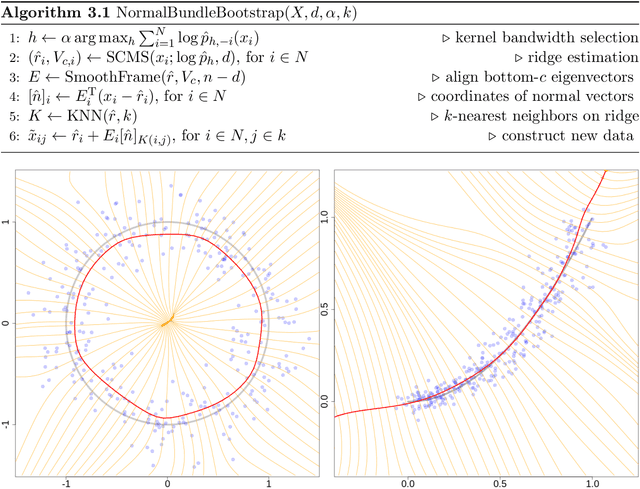
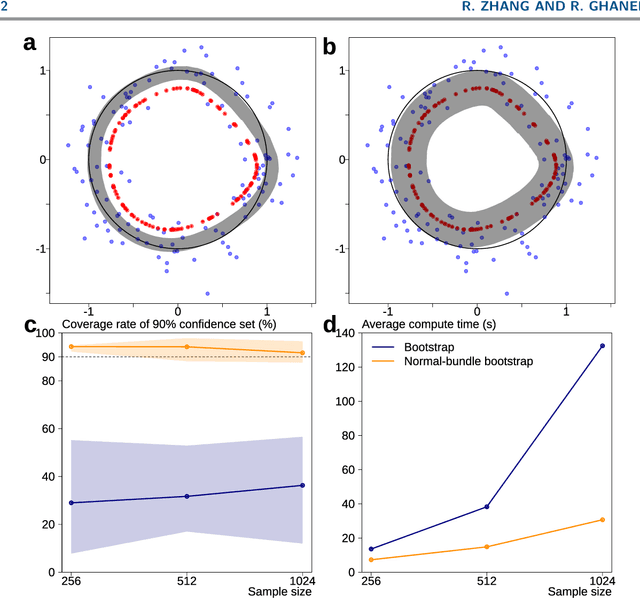
Probabilistic models of data sets often exhibit salient geometric structure. Such a phenomenon is summed up in the manifold distribution hypothesis, and can be exploited in probabilistic learning. Here we present normal-bundle bootstrap (NBB), a method that generates new data which preserve the geometric structure of a given data set. Inspired by algorithms for manifold learning and concepts in differential geometry, our method decomposes the underlying probability measure into a marginalized measure on a learned data manifold and conditional measures on the normal spaces. The algorithm estimates the data manifold as a density ridge, and constructs new data by bootstrapping projection vectors and adding them to the ridge. We apply our method to the inference of density ridge and related statistics, and data augmentation to reduce overfitting.