Gaussian Process Thompson Sampling via Rootfinding
Paper and Code
Oct 10, 2024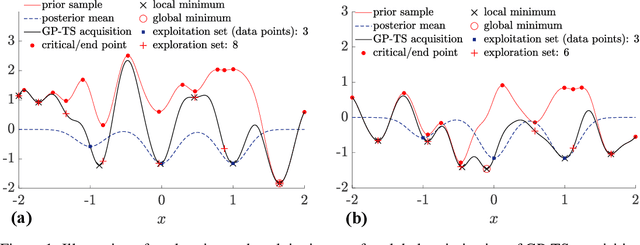
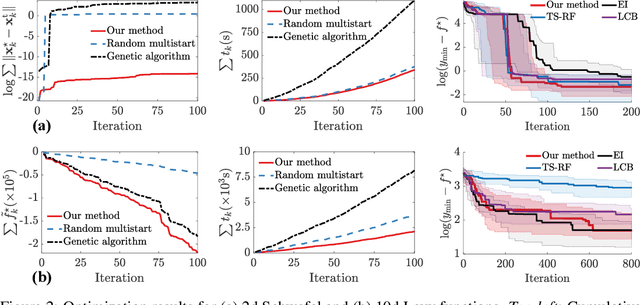
Thompson sampling (TS) is a simple, effective stochastic policy in Bayesian decision making. It samples the posterior belief about the reward profile and optimizes the sample to obtain a candidate decision. In continuous optimization, the posterior of the objective function is often a Gaussian process (GP), whose sample paths have numerous local optima, making their global optimization challenging. In this work, we introduce an efficient global optimization strategy for GP-TS that carefully selects starting points for gradient-based multi-start optimizers. It identifies all local optima of the prior sample via univariate global rootfinding, and optimizes the posterior sample using a differentiable, decoupled representation. We demonstrate remarkable improvement in the global optimization of GP posterior samples, especially in high dimensions. This leads to dramatic improvements in the overall performance of Bayesian optimization using GP-TS acquisition functions, surprisingly outperforming alternatives like GP-UCB and EI.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge