Optimizing Posterior Samples for Bayesian Optimization via Rootfinding
Paper and Code
Oct 29, 2024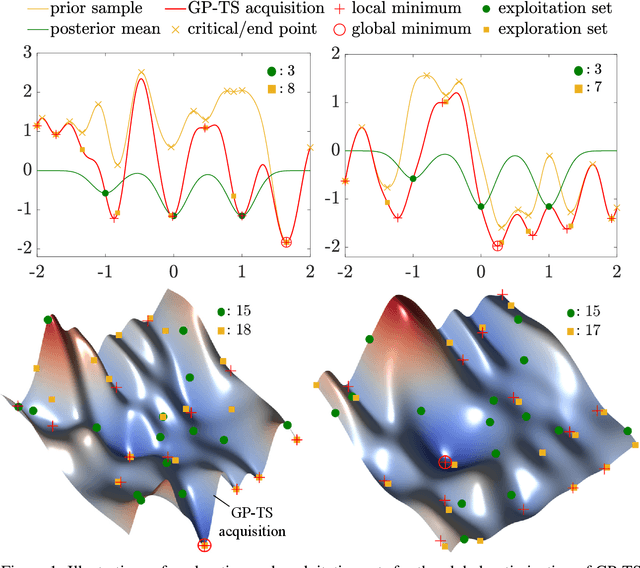
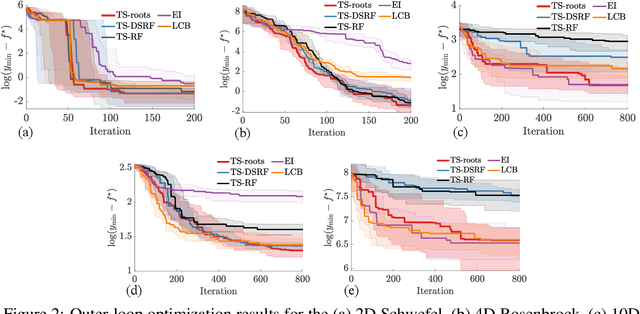
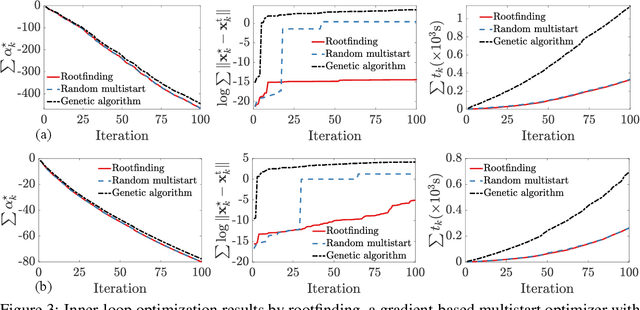
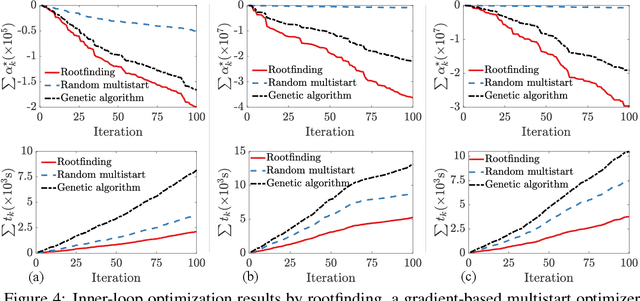
Bayesian optimization devolves the global optimization of a costly objective function to the global optimization of a sequence of acquisition functions. This inner-loop optimization can be catastrophically difficult if it involves posterior samples, especially in higher dimensions. We introduce an efficient global optimization strategy for posterior samples based on global rootfinding. It provides gradient-based optimizers with judiciously selected starting points, designed to combine exploitation and exploration. The algorithm scales practically linearly to high dimensions. For posterior sample-based acquisition functions such as Gaussian process Thompson sampling (GP-TS) and variants of entropy search, we demonstrate remarkable improvement in both inner- and outer-loop optimization, surprisingly outperforming alternatives like EI and GP-UCB in most cases. We also propose a sample-average formulation of GP-TS, which has a parameter to explicitly control exploitation and can be computed at the cost of one posterior sample. Our implementation is available at https://github.com/UQUH/TSRoots .
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge