Normal-bundle Bootstrap
Paper and Code
Jul 27, 2020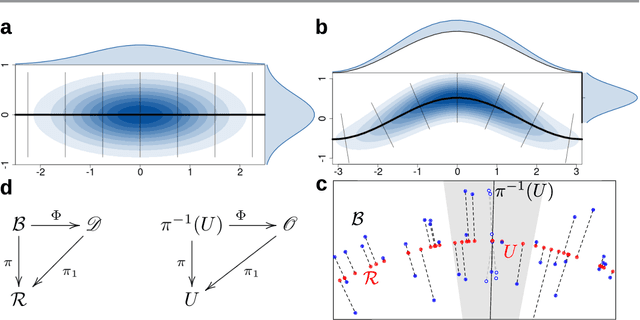
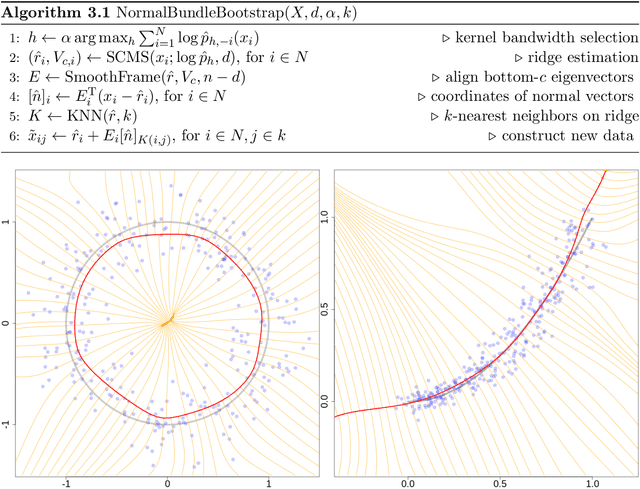
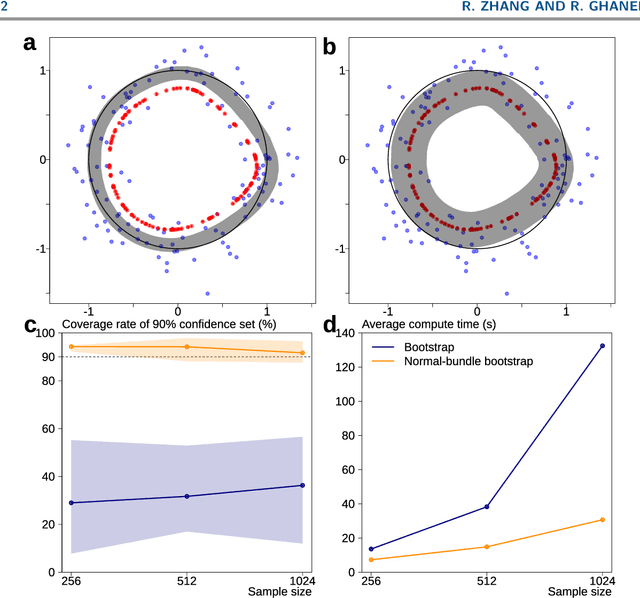

Probabilistic models of data sets often exhibit salient geometric structure. Such a phenomenon is summed up in the manifold distribution hypothesis, and can be exploited in probabilistic learning. Here we present normal-bundle bootstrap (NBB), a method that generates new data which preserve the geometric structure of a given data set. Inspired by algorithms for manifold learning and concepts in differential geometry, our method decomposes the underlying probability measure into a marginalized measure on a learned data manifold and conditional measures on the normal spaces. The algorithm estimates the data manifold as a density ridge, and constructs new data by bootstrapping projection vectors and adding them to the ridge. We apply our method to the inference of density ridge and related statistics, and data augmentation to reduce overfitting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge