Debolina Paul
Convex Clustering Redefined: Robust Learning with the Median of Means Estimator
Nov 12, 2025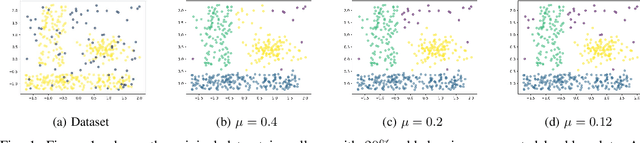
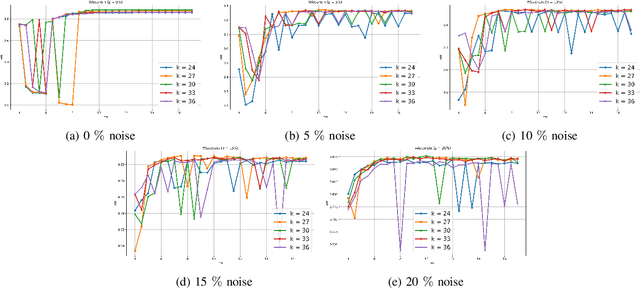
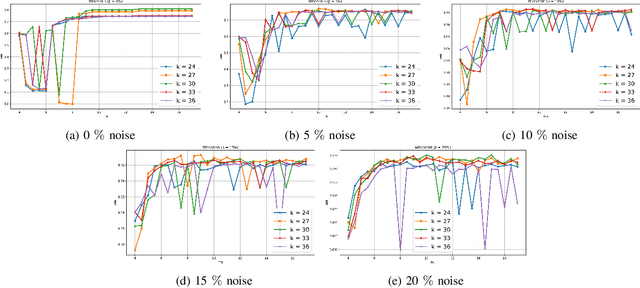
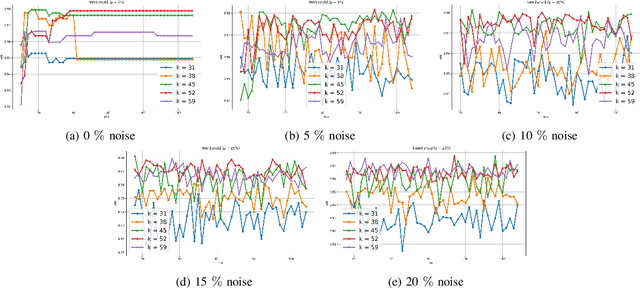
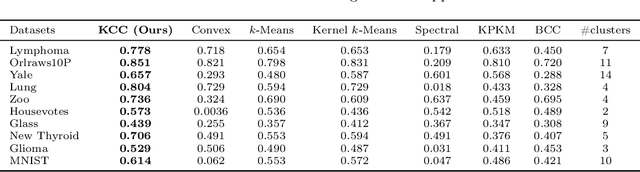
Abstract:Clustering approaches that utilize convex loss functions have recently attracted growing interest in the formation of compact data clusters. Although classical methods like k-means and its wide family of variants are still widely used, all of them require the number of clusters k to be supplied as input, and many are notably sensitive to initialization. Convex clustering provides a more stable alternative by formulating the clustering task as a convex optimization problem, ensuring a unique global solution. However, it faces challenges in handling high-dimensional data, especially in the presence of noise and outliers. Additionally, strong fusion regularization, controlled by the tuning parameter, can hinder effective cluster formation within a convex clustering framework. To overcome these challenges, we introduce a robust approach that integrates convex clustering with the Median of Means (MoM) estimator, thus developing an outlier-resistant and efficient clustering framework that does not necessitate prior knowledge of the number of clusters. By leveraging the robustness of MoM alongside the stability of convex clustering, our method enhances both performance and efficiency, especially on large-scale datasets. Theoretical analysis demonstrates weak consistency under specific conditions, while experiments on synthetic and real-world datasets validate the method's superior performance compared to existing approaches.
A New Framework for Convex Clustering in Kernel Spaces: Finite Sample Bounds, Consistency and Performance Insights
Nov 07, 2025

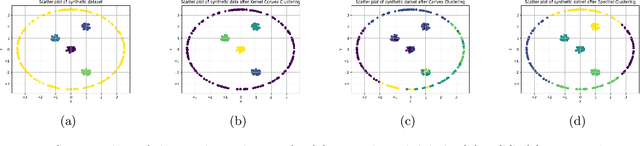
Abstract:Convex clustering is a well-regarded clustering method, resembling the similar centroid-based approach of Lloyd's $k$-means, without requiring a predefined cluster count. It starts with each data point as its centroid and iteratively merges them. Despite its advantages, this method can fail when dealing with data exhibiting linearly non-separable or non-convex structures. To mitigate the limitations, we propose a kernelized extension of the convex clustering method. This approach projects the data points into a Reproducing Kernel Hilbert Space (RKHS) using a feature map, enabling convex clustering in this transformed space. This kernelization not only allows for better handling of complex data distributions but also produces an embedding in a finite-dimensional vector space. We provide a comprehensive theoretical underpinnings for our kernelized approach, proving algorithmic convergence and establishing finite sample bounds for our estimates. The effectiveness of our method is demonstrated through extensive experiments on both synthetic and real-world datasets, showing superior performance compared to state-of-the-art clustering techniques. This work marks a significant advancement in the field, offering an effective solution for clustering in non-linear and non-convex data scenarios.
Robust and Automatic Data Clustering: Dirichlet Process meets Median-of-Means
Nov 26, 2023



Abstract:Clustering stands as one of the most prominent challenges within the realm of unsupervised machine learning. Among the array of centroid-based clustering algorithms, the classic $k$-means algorithm, rooted in Lloyd's heuristic, takes center stage as one of the extensively employed techniques in the literature. Nonetheless, both $k$-means and its variants grapple with noteworthy limitations. These encompass a heavy reliance on initial cluster centroids, susceptibility to converging into local minima of the objective function, and sensitivity to outliers and noise in the data. When confronted with data containing noisy or outlier-laden observations, the Median-of-Means (MoM) estimator emerges as a stabilizing force for any centroid-based clustering framework. On a different note, a prevalent constraint among existing clustering methodologies resides in the prerequisite knowledge of the number of clusters prior to analysis. Utilizing model-based methodologies, such as Bayesian nonparametric models, offers the advantage of infinite mixture models, thereby circumventing the need for such requirements. Motivated by these facts, in this article, we present an efficient and automatic clustering technique by integrating the principles of model-based and centroid-based methodologies that mitigates the effect of noise on the quality of clustering while ensuring that the number of clusters need not be specified in advance. Statistical guarantees on the upper bound of clustering error, and rigorous assessment through simulated and real datasets suggest the advantages of our proposed method over existing state-of-the-art clustering algorithms.
Robust Linear Predictions: Analyses of Uniform Concentration, Fast Rates and Model Misspecification
Jan 06, 2022
Abstract:The problem of linear predictions has been extensively studied for the past century under pretty generalized frameworks. Recent advances in the robust statistics literature allow us to analyze robust versions of classical linear models through the prism of Median of Means (MoM). Combining these approaches in a piecemeal way might lead to ad-hoc procedures, and the restricted theoretical conclusions that underpin each individual contribution may no longer be valid. To meet these challenges coherently, in this study, we offer a unified robust framework that includes a broad variety of linear prediction problems on a Hilbert space, coupled with a generic class of loss functions. Notably, we do not require any assumptions on the distribution of the outlying data points ($\mathcal{O}$) nor the compactness of the support of the inlying ones ($\mathcal{I}$). Under mild conditions on the dual norm, we show that for misspecification level $\epsilon$, these estimators achieve an error rate of $O(\max\left\{|\mathcal{O}|^{1/2}n^{-1/2}, |\mathcal{I}|^{1/2}n^{-1} \right\}+\epsilon)$, matching the best-known rates in literature. This rate is slightly slower than the classical rates of $O(n^{-1/2})$, indicating that we need to pay a price in terms of error rates to obtain robust estimates. Additionally, we show that this rate can be improved to achieve so-called ``fast rates" under additional assumptions.
Uniform Concentration Bounds toward a Unified Framework for Robust Clustering
Oct 27, 2021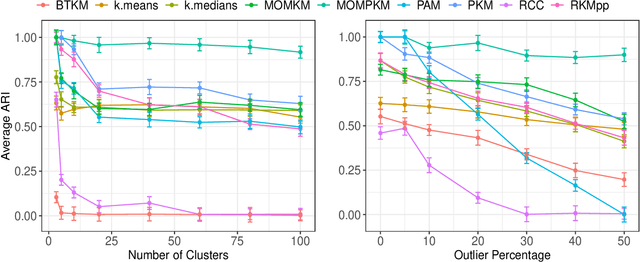

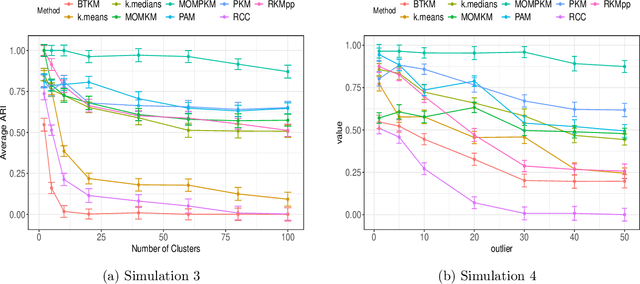
Abstract:Recent advances in center-based clustering continue to improve upon the drawbacks of Lloyd's celebrated $k$-means algorithm over $60$ years after its introduction. Various methods seek to address poor local minima, sensitivity to outliers, and data that are not well-suited to Euclidean measures of fit, but many are supported largely empirically. Moreover, combining such approaches in a piecemeal manner can result in ad hoc methods, and the limited theoretical results supporting each individual contribution may no longer hold. Toward addressing these issues in a principled way, this paper proposes a cohesive robust framework for center-based clustering under a general class of dissimilarity measures. In particular, we present a rigorous theoretical treatment within a Median-of-Means (MoM) estimation framework, showing that it subsumes several popular $k$-means variants. In addition to unifying existing methods, we derive uniform concentration bounds that complete their analyses, and bridge these results to the MoM framework via Dudley's chaining arguments. Importantly, we neither require any assumptions on the distribution of the outlying observations nor on the relative number of observations $n$ to features $p$. We establish strong consistency and an error rate of $O(n^{-1/2})$ under mild conditions, surpassing the best-known results in the literature. The methods are empirically validated thoroughly on real and synthetic datasets.
Robust Principal Component Analysis: A Median of Means Approach
Feb 05, 2021



Abstract:Principal Component Analysis (PCA) is a fundamental tool for data visualization, denoising, and dimensionality reduction. It is widely popular in Statistics, Machine Learning, Computer Vision, and related fields. However, PCA is well known to fall prey to the presence of outliers and often fails to detect the true underlying low-dimensional structure within the dataset. Recent supervised learning methods, following the Median of Means (MoM) philosophy, have shown great success in dealing with outlying observations without much compromise to their large sample theoretical properties. In this paper, we propose a PCA procedure based on the MoM principle. Called the Median of Means Principal Component Analysis (MoMPCA), the proposed method is not only computationally appealing but also achieves optimal convergence rates under minimal assumptions. In particular, we explore the non-asymptotic error bounds of the obtained solution via the aid of Vapnik-Chervonenkis theory and Rademacher complexity, while granting absolutely no assumption on the outlying observations. The efficacy of the proposal is also thoroughly showcased through simulations and real data applications.
Automated Clustering of High-dimensional Data with a Feature Weighted Mean Shift Algorithm
Dec 20, 2020



Abstract:Mean shift is a simple interactive procedure that gradually shifts data points towards the mode which denotes the highest density of data points in the region. Mean shift algorithms have been effectively used for data denoising, mode seeking, and finding the number of clusters in a dataset in an automated fashion. However, the merits of mean shift quickly fade away as the data dimensions increase and only a handful of features contain useful information about the cluster structure of the data. We propose a simple yet elegant feature-weighted variant of mean shift to efficiently learn the feature importance and thus, extending the merits of mean shift to high-dimensional data. The resulting algorithm not only outperforms the conventional mean shift clustering procedure but also preserves its computational simplicity. In addition, the proposed method comes with rigorous theoretical convergence guarantees and a convergence rate of at least a cubic order. The efficacy of our proposal is thoroughly assessed through experimental comparison against baseline and state-of-the-art clustering methods on synthetic as well as real-world datasets.
Kernel k-Means, By All Means: Algorithms and Strong Consistency
Nov 12, 2020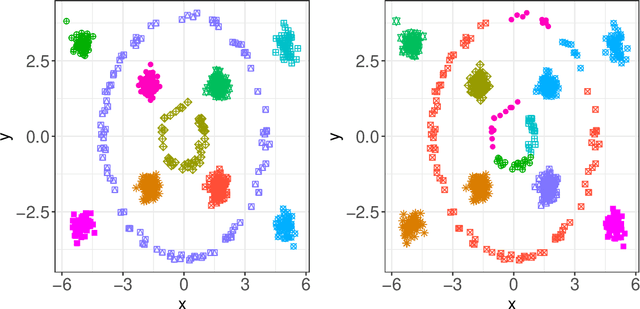

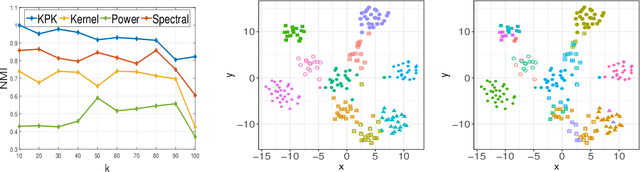

Abstract:Kernel $k$-means clustering is a powerful tool for unsupervised learning of non-linearly separable data. Since the earliest attempts, researchers have noted that such algorithms often become trapped by local minima arising from non-convexity of the underlying objective function. In this paper, we generalize recent results leveraging a general family of means to combat sub-optimal local solutions to the kernel and multi-kernel settings. Called Kernel Power $k$-Means, our algorithm makes use of majorization-minimization (MM) to better solve this non-convex problem. We show the method implicitly performs annealing in kernel feature space while retaining efficient, closed-form updates, and we rigorously characterize its convergence properties both from computational and statistical points of view. In particular, we characterize the large sample behavior of the proposed method by establishing strong consistency guarantees. Its merits are thoroughly validated on a suite of simulated datasets and real data benchmarks that feature non-linear and multi-view separation.
Principal Ellipsoid Analysis (PEA): Efficient non-linear dimension reduction & clustering
Sep 07, 2020

Abstract:Even with the rise in popularity of over-parameterized models, simple dimensionality reduction and clustering methods, such as PCA and k-means, are still routinely used in an amazing variety of settings. A primary reason is the combination of simplicity, interpretability and computational efficiency. The focus of this article is on improving upon PCA and k-means, by allowing non-linear relations in the data and more flexible cluster shapes, without sacrificing the key advantages. The key contribution is a new framework for Principal Elliptical Analysis (PEA), defining a simple and computationally efficient alternative to PCA that fits the best elliptical approximation through the data. We provide theoretical guarantees on the proposed PEA algorithm using Vapnik-Chervonenkis (VC) theory to show strong consistency and uniform concentration bounds. Toy experiments illustrate the performance of PEA, and the ability to adapt to non-linear structure and complex cluster shapes. In a rich variety of real data clustering applications, PEA is shown to do as well as k-means for simple datasets, while dramatically improving performance in more complex settings.
Entropy Regularized Power k-Means Clustering
Jan 10, 2020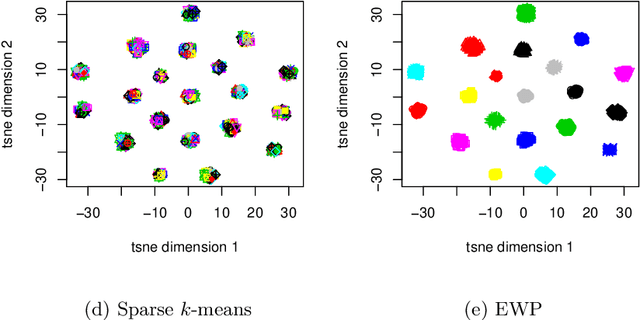
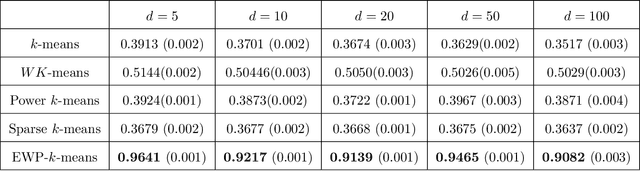
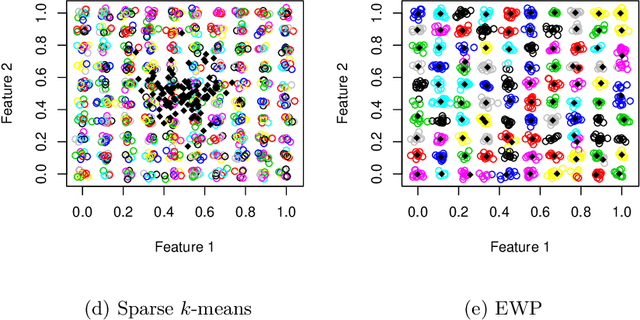
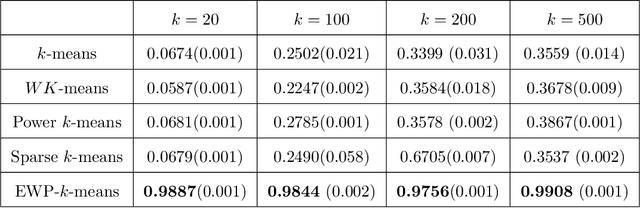
Abstract:Despite its well-known shortcomings, $k$-means remains one of the most widely used approaches to data clustering. Current research continues to tackle its flaws while attempting to preserve its simplicity. Recently, the \textit{power $k$-means} algorithm was proposed to avoid trapping in local minima by annealing through a family of smoother surfaces. However, the approach lacks theoretical justification and fails in high dimensions when many features are irrelevant. This paper addresses these issues by introducing \textit{entropy regularization} to learn feature relevance while annealing. We prove consistency of the proposed approach and derive a scalable majorization-minimization algorithm that enjoys closed-form updates and convergence guarantees. In particular, our method retains the same computational complexity of $k$-means and power $k$-means, but yields significant improvements over both. Its merits are thoroughly assessed on a suite of real and synthetic data experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge