Entropy Regularized Power k-Means Clustering
Paper and Code
Jan 10, 2020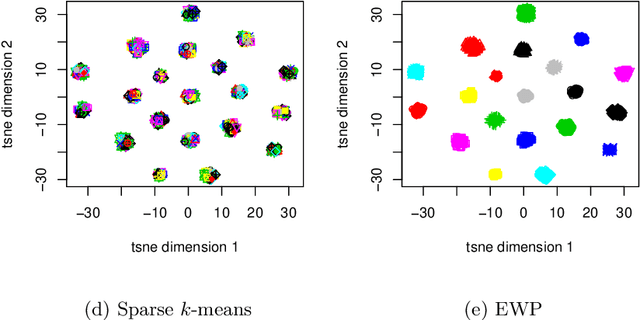
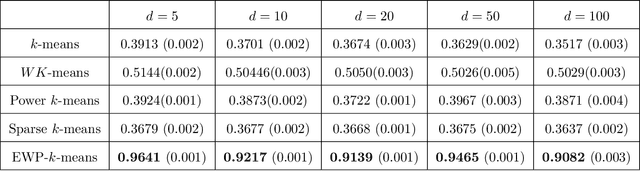
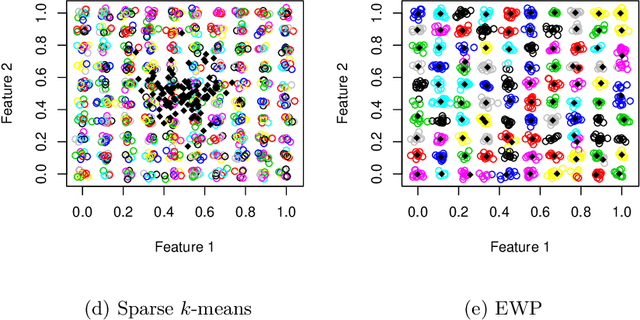
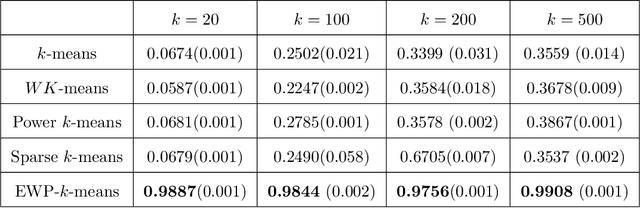
Despite its well-known shortcomings, $k$-means remains one of the most widely used approaches to data clustering. Current research continues to tackle its flaws while attempting to preserve its simplicity. Recently, the \textit{power $k$-means} algorithm was proposed to avoid trapping in local minima by annealing through a family of smoother surfaces. However, the approach lacks theoretical justification and fails in high dimensions when many features are irrelevant. This paper addresses these issues by introducing \textit{entropy regularization} to learn feature relevance while annealing. We prove consistency of the proposed approach and derive a scalable majorization-minimization algorithm that enjoys closed-form updates and convergence guarantees. In particular, our method retains the same computational complexity of $k$-means and power $k$-means, but yields significant improvements over both. Its merits are thoroughly assessed on a suite of real and synthetic data experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge