Swagatam Das
ARREST: Adversarial Resilient Regulation Enhancing Safety and Truth in Large Language Models
Jan 07, 2026Abstract:Human cognition, driven by complex neurochemical processes, oscillates between imagination and reality and learns to self-correct whenever such subtle drifts lead to hallucinations or unsafe associations. In recent years, LLMs have demonstrated remarkable performance in a wide range of tasks. However, they still lack human cognition to balance factuality and safety. Bearing the resemblance, we argue that both factual and safety failures in LLMs arise from a representational misalignment in their latent activation space, rather than addressing those as entirely separate alignment issues. We hypothesize that an external network, trained to understand the fluctuations, can selectively intervene in the model to regulate falsehood into truthfulness and unsafe output into safe output without fine-tuning the model parameters themselves. Reflecting the hypothesis, we propose ARREST (Adversarial Resilient Regulation Enhancing Safety and Truth), a unified framework that identifies and corrects drifted features, engaging both soft and hard refusals in addition to factual corrections. Our empirical results show that ARREST not only regulates misalignment but is also more versatile compared to the RLHF-aligned models in generating soft refusals due to adversarial training. We make our codebase available at https://github.com/sharanya-dasgupta001/ARREST.
Hyperbolic Gaussian Blurring Mean Shift: A Statistical Mode-Seeking Framework for Clustering in Curved Spaces
Dec 12, 2025Abstract:Clustering is a fundamental unsupervised learning task for uncovering patterns in data. While Gaussian Blurring Mean Shift (GBMS) has proven effective for identifying arbitrarily shaped clusters in Euclidean space, it struggles with datasets exhibiting hierarchical or tree-like structures. In this work, we introduce HypeGBMS, a novel extension of GBMS to hyperbolic space. Our method replaces Euclidean computations with hyperbolic distances and employs Möbius-weighted means to ensure that all updates remain consistent with the geometry of the space. HypeGBMS effectively captures latent hierarchies while retaining the density-seeking behavior of GBMS. We provide theoretical insights into convergence and computational complexity, along with empirical results that demonstrate improved clustering quality in hierarchical datasets. This work bridges classical mean-shift clustering and hyperbolic representation learning, offering a principled approach to density-based clustering in curved spaces. Extensive experimental evaluations on $11$ real-world datasets demonstrate that HypeGBMS significantly outperforms conventional mean-shift clustering methods in non-Euclidean settings, underscoring its robustness and effectiveness.
HalluShift++: Bridging Language and Vision through Internal Representation Shifts for Hierarchical Hallucinations in MLLMs
Dec 08, 2025Abstract:Multimodal Large Language Models (MLLMs) have demonstrated remarkable capabilities in vision-language understanding tasks. While these models often produce linguistically coherent output, they often suffer from hallucinations, generating descriptions that are factually inconsistent with the visual content, potentially leading to adverse consequences. Therefore, the assessment of hallucinations in MLLM has become increasingly crucial in the model development process. Contemporary methodologies predominantly depend on external LLM evaluators, which are themselves susceptible to hallucinations and may present challenges in terms of domain adaptation. In this study, we propose the hypothesis that hallucination manifests as measurable irregularities within the internal layer dynamics of MLLMs, not merely due to distributional shifts but also in the context of layer-wise analysis of specific assumptions. By incorporating such modifications, \textsc{\textsc{HalluShift++}} broadens the efficacy of hallucination detection from text-based large language models (LLMs) to encompass multimodal scenarios. Our codebase is available at https://github.com/C0mRD/HalluShift_Plus.
Convex Clustering Redefined: Robust Learning with the Median of Means Estimator
Nov 12, 2025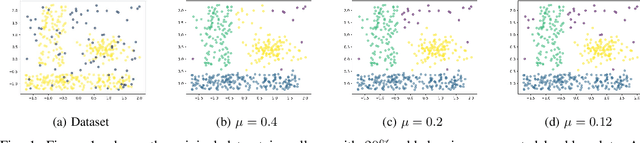
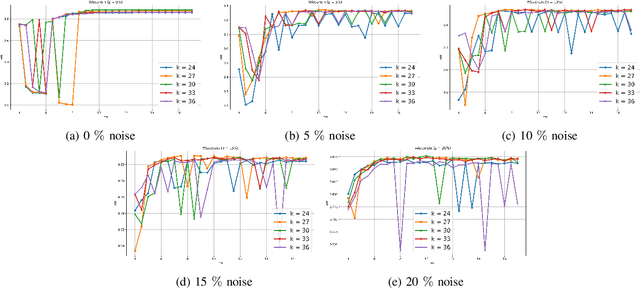
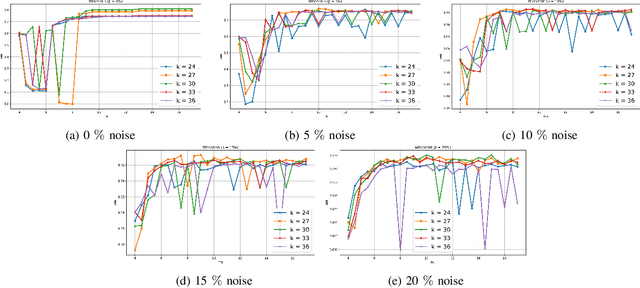
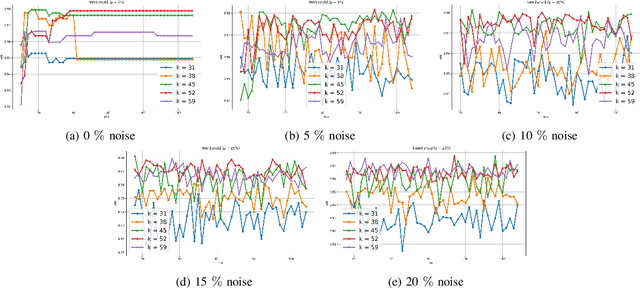
Abstract:Clustering approaches that utilize convex loss functions have recently attracted growing interest in the formation of compact data clusters. Although classical methods like k-means and its wide family of variants are still widely used, all of them require the number of clusters k to be supplied as input, and many are notably sensitive to initialization. Convex clustering provides a more stable alternative by formulating the clustering task as a convex optimization problem, ensuring a unique global solution. However, it faces challenges in handling high-dimensional data, especially in the presence of noise and outliers. Additionally, strong fusion regularization, controlled by the tuning parameter, can hinder effective cluster formation within a convex clustering framework. To overcome these challenges, we introduce a robust approach that integrates convex clustering with the Median of Means (MoM) estimator, thus developing an outlier-resistant and efficient clustering framework that does not necessitate prior knowledge of the number of clusters. By leveraging the robustness of MoM alongside the stability of convex clustering, our method enhances both performance and efficiency, especially on large-scale datasets. Theoretical analysis demonstrates weak consistency under specific conditions, while experiments on synthetic and real-world datasets validate the method's superior performance compared to existing approaches.
A New Framework for Convex Clustering in Kernel Spaces: Finite Sample Bounds, Consistency and Performance Insights
Nov 07, 2025

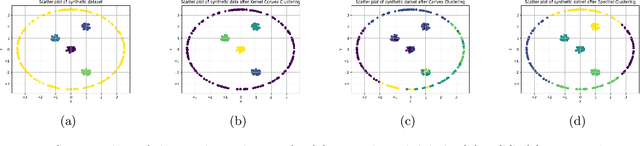
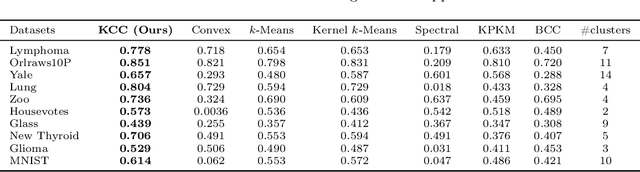
Abstract:Convex clustering is a well-regarded clustering method, resembling the similar centroid-based approach of Lloyd's $k$-means, without requiring a predefined cluster count. It starts with each data point as its centroid and iteratively merges them. Despite its advantages, this method can fail when dealing with data exhibiting linearly non-separable or non-convex structures. To mitigate the limitations, we propose a kernelized extension of the convex clustering method. This approach projects the data points into a Reproducing Kernel Hilbert Space (RKHS) using a feature map, enabling convex clustering in this transformed space. This kernelization not only allows for better handling of complex data distributions but also produces an embedding in a finite-dimensional vector space. We provide a comprehensive theoretical underpinnings for our kernelized approach, proving algorithmic convergence and establishing finite sample bounds for our estimates. The effectiveness of our method is demonstrated through extensive experiments on both synthetic and real-world datasets, showing superior performance compared to state-of-the-art clustering techniques. This work marks a significant advancement in the field, offering an effective solution for clustering in non-linear and non-convex data scenarios.
A Free Probabilistic Framework for Denoising Diffusion Models: Entropy, Transport, and Reverse Processes
Oct 26, 2025Abstract:This work develops a rigorous framework for diffusion-based generative modeling in the setting of free probability. We extend classical denoising diffusion probabilistic models to free diffusion processes -- stochastic dynamics acting on noncommutative random variables whose spectral measures evolve by free additive convolution. The forward dynamics satisfy a free Fokker--Planck equation that increases Voiculescu's free entropy and dissipates free Fisher information, providing a noncommutative analogue of the classical de Bruijn identity. Using tools from free stochastic analysis, including a free Malliavin calculus and a Clark--Ocone representation, we derive the reverse-time stochastic differential equation driven by the conjugate variable, the free analogue of the score function. We further develop a variational formulation of these flows in the free Wasserstein space, showing that the resulting gradient-flow structure converges to the semicircular equilibrium law. Together, these results connect modern diffusion models with the information geometry of free entropy and establish a mathematical foundation for generative modeling with operator-valued or high-dimensional structured data.
APFEx: Adaptive Pareto Front Explorer for Intersectional Fairness
Sep 17, 2025Abstract:Ensuring fairness in machine learning models is critical, especially when biases compound across intersecting protected attributes like race, gender, and age. While existing methods address fairness for single attributes, they fail to capture the nuanced, multiplicative biases faced by intersectional subgroups. We introduce Adaptive Pareto Front Explorer (APFEx), the first framework to explicitly model intersectional fairness as a joint optimization problem over the Cartesian product of sensitive attributes. APFEx combines three key innovations- (1) an adaptive multi-objective optimizer that dynamically switches between Pareto cone projection, gradient weighting, and exploration strategies to navigate fairness-accuracy trade-offs, (2) differentiable intersectional fairness metrics enabling gradient-based optimization of non-smooth subgroup disparities, and (3) theoretical guarantees of convergence to Pareto-optimal solutions. Experiments on four real-world datasets demonstrate APFEx's superiority, reducing fairness violations while maintaining competitive accuracy. Our work bridges a critical gap in fair ML, providing a scalable, model-agnostic solution for intersectional fairness.
Learning from Heterophilic Graphs: A Spectral Theory Perspective on the Impact of Self-Loops and Parallel Edges
Sep 16, 2025Abstract:Graph heterophily poses a formidable challenge to the performance of Message-passing Graph Neural Networks (MP-GNNs). The familiar low-pass filters like Graph Convolutional Networks (GCNs) face performance degradation, which can be attributed to the blending of the messages from dissimilar neighboring nodes. The performance of the low-pass filters on heterophilic graphs still requires an in-depth analysis. In this context, we update the heterophilic graphs by adding a number of self-loops and parallel edges. We observe that eigenvalues of the graph Laplacian decrease and increase respectively by increasing the number of self-loops and parallel edges. We conduct several studies regarding the performance of GCN on various benchmark heterophilic networks by adding either self-loops or parallel edges. The studies reveal that the GCN exhibited either increasing or decreasing performance trends on adding self-loops and parallel edges. In light of the studies, we established connections between the graph spectra and the performance trends of the low-pass filters on the heterophilic graphs. The graph spectra characterize the essential intrinsic properties of the input graph like the presence of connected components, sparsity, average degree, cluster structures, etc. Our work is adept at seamlessly evaluating graph spectrum and properties by observing the performance trends of the low-pass filters without pursuing the costly eigenvalue decomposition. The theoretical foundations are also discussed to validate the impact of adding self-loops and parallel edges on the graph spectrum.
Grounding the Ungrounded: A Spectral-Graph Framework for Quantifying Hallucinations in multimodal LLMs
Aug 26, 2025Abstract:Hallucinations in large language models (LLMs) remain a fundamental obstacle to trustworthy AI, particularly in high-stakes multimodal domains such as medicine, law, and finance. Existing evaluation techniques are largely heuristic -- anchored in qualitative benchmarking or ad-hoc empirical mitigation -- providing neither principled quantification nor actionable theoretical guarantees. This gap leaves a critical blind spot in understanding how hallucinations arise, propagate, and interact across modalities. We introduce the first (to our knowledge) rigorous information geometric framework in diffusion dynamics for quantifying hallucinations in multimodal LLMs (MLLMs), advancing the field from qualitative detection to mathematically grounded measurement. Our approach represents MLLM outputs as the spectral embeddings over multimodal graph Laplacians and characterizes the manifold gaps of truth vs inconsistencies as the semantic distortion, enabling the tight Rayleigh--Ritz bounds on the multimodal hallucination energy as a functional of time-dependent temperature profiles. By leveraging eigenmode decompositions in Reproducing Kernel Hilbert Space (RKHS) embeddings, our framework delivers modality-aware, theoretically interpretable metrics that capture the evolution of hallucinations across time and input prompts through temperature annealing. This work establishes a principled foundation for quantifying and bounding hallucinations, transforming them from a qualitative risk to a tractable, analyzable phenomenon.
Relation-Aware Slicing in Cross-Domain Alignment
Jul 17, 2025Abstract:The Sliced Gromov-Wasserstein (SGW) distance, aiming to relieve the computational cost of solving a non-convex quadratic program that is the Gromov-Wasserstein distance, utilizes projecting directions sampled uniformly from unit hyperspheres. This slicing mechanism incurs unnecessary computational costs due to uninformative directions, which also affects the representative power of the distance. However, finding a more appropriate distribution over the projecting directions (slicing distribution) is often an optimization problem in itself that comes with its own computational cost. In addition, with more intricate distributions, the sampling itself may be expensive. As a remedy, we propose an optimization-free slicing distribution that provides fast sampling for the Monte Carlo approximation. We do so by introducing the Relation-Aware Projecting Direction (RAPD), effectively capturing the pairwise association of each of two pairs of random vectors, each following their ambient law. This enables us to derive the Relation-Aware Slicing Distribution (RASD), a location-scale law corresponding to sampled RAPDs. Finally, we introduce the RASGW distance and its variants, e.g., IWRASGW (Importance Weighted RASGW), which overcome the shortcomings experienced by SGW. We theoretically analyze its properties and substantiate its empirical prowess using extensive experiments on various alignment tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge