Fortifying Fully Convolutional Generative Adversarial Networks for Image Super-Resolution Using Divergence Measures

Super-Resolution (SR) is a time-hallowed image processing problem that aims to improve the quality of a Low-Resolution (LR) sample up to the standard of its High-Resolution (HR) counterpart. We aim to address this by introducing Super-Resolution Generator (SuRGe), a fully-convolutional Generative Adversarial Network (GAN)-based architecture for SR. We show that distinct convolutional features obtained at increasing depths of a GAN generator can be optimally combined by a set of learnable convex weights to improve the quality of generated SR samples. In the process, we employ the Jensen-Shannon and the Gromov-Wasserstein losses respectively between the SR-HR and LR-SR pairs of distributions to further aid the generator of SuRGe to better exploit the available information in an attempt to improve SR. Moreover, we train the discriminator of SuRGe with the Wasserstein loss with gradient penalty, to primarily prevent mode collapse. The proposed SuRGe, as an end-to-end GAN workflow tailor-made for super-resolution, offers improved performance while maintaining low inference time. The efficacy of SuRGe is substantiated by its superior performance compared to 18 state-of-the-art contenders on 10 benchmark datasets.

Concurrent Density Estimation with Wasserstein Autoencoders: Some Statistical Insights

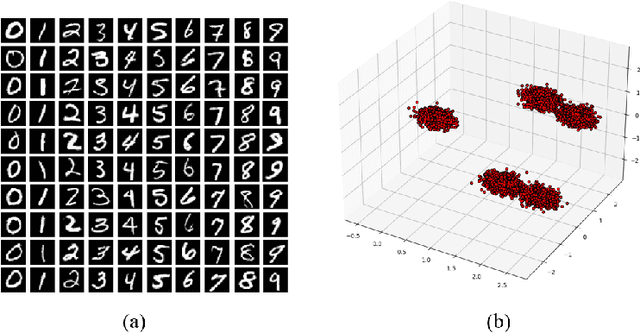
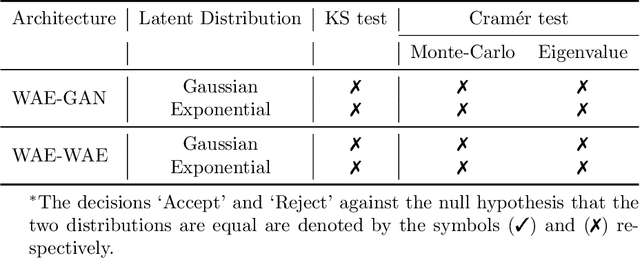
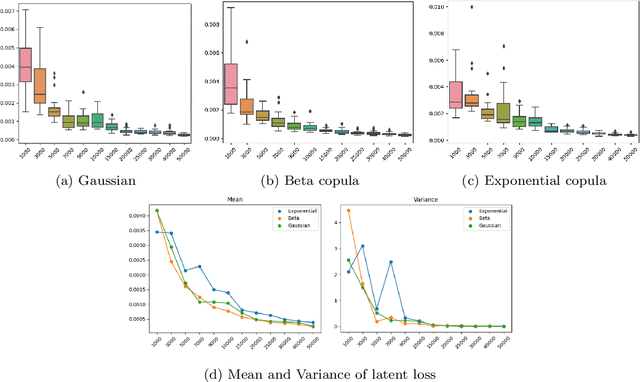
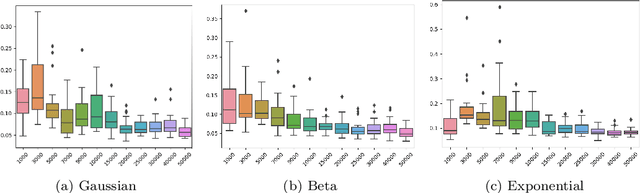
Variational Autoencoders (VAEs) have been a pioneering force in the realm of deep generative models. Amongst its legions of progenies, Wasserstein Autoencoders (WAEs) stand out in particular due to the dual offering of heightened generative quality and a strong theoretical backbone. WAEs consist of an encoding and a decoding network forming a bottleneck with the prime objective of generating new samples resembling the ones it was catered to. In the process, they aim to achieve a target latent representation of the encoded data. Our work is an attempt to offer a theoretical understanding of the machinery behind WAEs. From a statistical viewpoint, we pose the problem as concurrent density estimation tasks based on neural network-induced transformations. This allows us to establish deterministic upper bounds on the realized errors WAEs commit. We also analyze the propagation of these stochastic errors in the presence of adversaries. As a result, both the large sample properties of the reconstructed distribution and the resilience of WAE models are explored.

Statistical Regeneration Guarantees of the Wasserstein Autoencoder with Latent Space Consistency

The introduction of Variational Autoencoders (VAE) has been marked as a breakthrough in the history of representation learning models. Besides having several accolades of its own, VAE has successfully flagged off a series of inventions in the form of its immediate successors. Wasserstein Autoencoder (WAE), being an heir to that realm carries with it all of the goodness and heightened generative promises, matching even the generative adversarial networks (GANs). Needless to say, recent years have witnessed a remarkable resurgence in statistical analyses of the GANs. Similar examinations for Autoencoders, however, despite their diverse applicability and notable empirical performance, remain largely absent. To close this gap, in this paper, we investigate the statistical properties of WAE. Firstly, we provide statistical guarantees that WAE achieves the target distribution in the latent space, utilizing the Vapnik Chervonenkis (VC) theory. The main result, consequently ensures the regeneration of the input distribution, harnessing the potential offered by Optimal Transport of measures under the Wasserstein metric. This study, in turn, hints at the class of distributions WAE can reconstruct after suffering a compression in the form of a latent law.