Kernel k-Means, By All Means: Algorithms and Strong Consistency
Paper and Code
Nov 12, 2020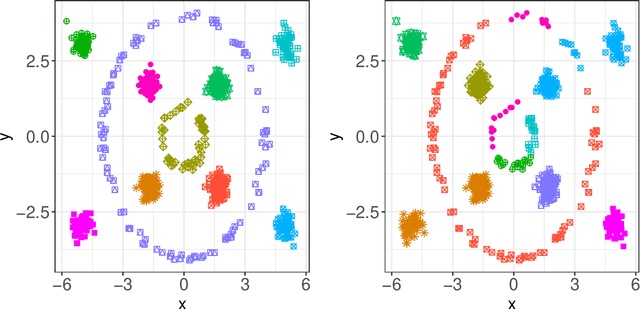

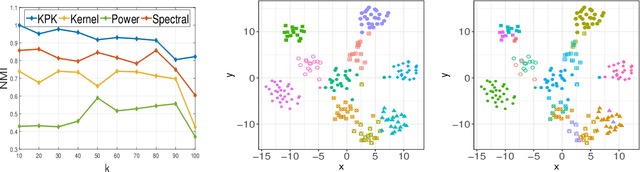

Kernel $k$-means clustering is a powerful tool for unsupervised learning of non-linearly separable data. Since the earliest attempts, researchers have noted that such algorithms often become trapped by local minima arising from non-convexity of the underlying objective function. In this paper, we generalize recent results leveraging a general family of means to combat sub-optimal local solutions to the kernel and multi-kernel settings. Called Kernel Power $k$-Means, our algorithm makes use of majorization-minimization (MM) to better solve this non-convex problem. We show the method implicitly performs annealing in kernel feature space while retaining efficient, closed-form updates, and we rigorously characterize its convergence properties both from computational and statistical points of view. In particular, we characterize the large sample behavior of the proposed method by establishing strong consistency guarantees. Its merits are thoroughly validated on a suite of simulated datasets and real data benchmarks that feature non-linear and multi-view separation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge