Local transfer learning Gaussian process modeling, with applications to surrogate modeling of expensive computer simulators
Paper and Code
Oct 17, 2024

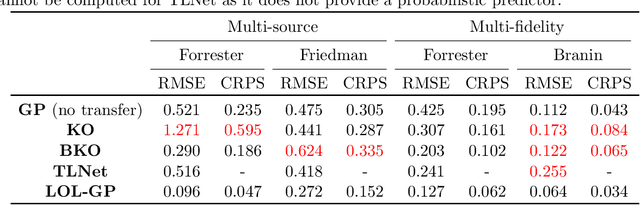

A critical bottleneck for scientific progress is the costly nature of computer simulations for complex systems. Surrogate models provide an appealing solution: such models are trained on simulator evaluations, then used to emulate and quantify uncertainty on the expensive simulator at unexplored inputs. In many applications, one often has available data on related systems. For example, in designing a new jet turbine, there may be existing studies on turbines with similar configurations. A key question is how information from such "source" systems can be transferred for effective surrogate training on the "target" system of interest. We thus propose a new LOcal transfer Learning Gaussian Process (LOL-GP) model, which leverages a carefully-designed Gaussian process to transfer such information for surrogate modeling. The key novelty of the LOL-GP is a latent regularization model, which identifies regions where transfer should be performed and regions where it should be avoided. This "local transfer" property is desirable in scientific systems: at certain parameters, such systems may behave similarly and thus transfer is beneficial; at other parameters, they may behave differently and thus transfer is detrimental. By accounting for local transfer, the LOL-GP can rectify a critical limitation of "negative transfer" in existing transfer learning models, where the transfer of information worsens predictive performance. We derive a Gibbs sampling algorithm for efficient posterior predictive sampling on the LOL-GP, for both the multi-source and multi-fidelity transfer settings. We then show, via a suite of numerical experiments and an application for jet turbine design, the improved surrogate performance of the LOL-GP over existing methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge