Scene-Driven Multimodal Knowledge Graph Construction for Embodied AI

Embodied AI is one of the most popular studies in artificial intelligence and robotics, which can effectively improve the intelligence of real-world agents (i.e. robots) serving human beings. Scene knowledge is important for an agent to understand the surroundings and make correct decisions in the varied open world. Currently, knowledge base for embodied tasks is missing and most existing work use general knowledge base or pre-trained models to enhance the intelligence of an agent. For conventional knowledge base, it is sparse, insufficient in capacity and cost in data collection. For pre-trained models, they face the uncertainty of knowledge and hard maintenance. To overcome the challenges of scene knowledge, we propose a scene-driven multimodal knowledge graph (Scene-MMKG) construction method combining conventional knowledge engineering and large language models. A unified scene knowledge injection framework is introduced for knowledge representation. To evaluate the advantages of our proposed method, we instantiate Scene-MMKG considering typical indoor robotic functionalities (Manipulation and Mobility), named ManipMob-MMKG. Comparisons in characteristics indicate our instantiated ManipMob-MMKG has broad superiority in data-collection efficiency and knowledge quality. Experimental results on typical embodied tasks show that knowledge-enhanced methods using our instantiated ManipMob-MMKG can improve the performance obviously without re-designing model structures complexly. Our project can be found at https://sites.google.com/view/manipmob-mmkg

Detecting Electricity Service Equity Issues with Transfer Counterfactual Learning on Large-Scale Outage Datasets

Energy justice is a growing area of interest in interdisciplinary energy research. However, identifying systematic biases in the energy sector remains challenging due to confounding variables, intricate heterogeneity in treatment effects, and limited data availability. To address these challenges, we introduce a novel approach for counterfactual causal analysis centered on energy justice. We use subgroup analysis to manage diverse factors and leverage the idea of transfer learning to mitigate data scarcity in each subgroup. In our numerical analysis, we apply our method to a large-scale customer-level power outage data set and investigate the counterfactual effect of demographic factors, such as income and age of the population, on power outage durations. Our results indicate that low-income and elderly-populated areas consistently experience longer power outages, regardless of weather conditions. This points to existing biases in the power system and highlights the need for focused improvements in areas with economic challenges.

ATMS: Algorithmic Trading-Guided Market Simulation

The effective construction of an Algorithmic Trading (AT) strategy often relies on market simulators, which remains challenging due to existing methods' inability to adapt to the sequential and dynamic nature of trading activities. This work fills this gap by proposing a metric to quantify market discrepancy. This metric measures the difference between a causal effect from underlying market unique characteristics and it is evaluated through the interaction between the AT agent and the market. Most importantly, we introduce Algorithmic Trading-guided Market Simulation (ATMS) by optimizing our proposed metric. Inspired by SeqGAN, ATMS formulates the simulator as a stochastic policy in reinforcement learning (RL) to account for the sequential nature of trading. Moreover, ATMS utilizes the policy gradient update to bypass differentiating the proposed metric, which involves non-differentiable operations such as order deletion from the market. Through extensive experiments on semi-real market data, we demonstrate the effectiveness of our metric and show that ATMS generates market data with improved similarity to reality compared to the state-of-the-art conditional Wasserstein Generative Adversarial Network (cWGAN) approach. Furthermore, ATMS produces market data with more balanced BUY and SELL volumes, mitigating the bias of the cWGAN baseline approach, where a simple strategy can exploit the BUY/SELL imbalance for profit.

Transfer Causal Learning: Causal Effect Estimation with Knowledge Transfer

A novel problem of improving causal effect estimation accuracy with the help of knowledge transfer under the same covariate (or feature) space setting, i.e., homogeneous transfer learning (TL), is studied, referred to as the Transfer Causal Learning (TCL) problem. While most recent efforts in adapting TL techniques to estimate average causal effect (ACE) have been focused on the heterogeneous covariate space setting, those methods are inadequate for tackling the TCL problem since their algorithm designs are based on the decomposition into shared and domain-specific covariate spaces. To address this issue, we propose a generic framework called $\ell_1$-TCL, which incorporates $\ell_1$ regularized TL for nuisance parameter estimation and downstream plug-in ACE estimators, including outcome regression, inverse probability weighted, and doubly robust estimators. Most importantly, with the help of Lasso for high-dimensional regression, we establish non-asymptotic recovery guarantees for the generalized linear model (GLM) under the sparsity assumption for the proposed $\ell_1$-TCL. From an empirical perspective, $\ell_1$-TCL is a generic learning framework that can incorporate not only GLM but also many recently developed non-parametric methods, which can enhance robustness to model mis-specification. We demonstrate this empirical benefit through extensive numerical simulation by incorporating both GLM and recent neural network-based approaches in $\ell_1$-TCL, which shows improved performance compared with existing TL approaches for ACE estimation. Furthermore, our $\ell_1$-TCL framework is subsequently applied to a real study, revealing that vasopressor therapy could prevent 28-day mortality within septic patients, which all baseline approaches fail to show.

Causal Graph Discovery from Self and Mutually Exciting Time Series

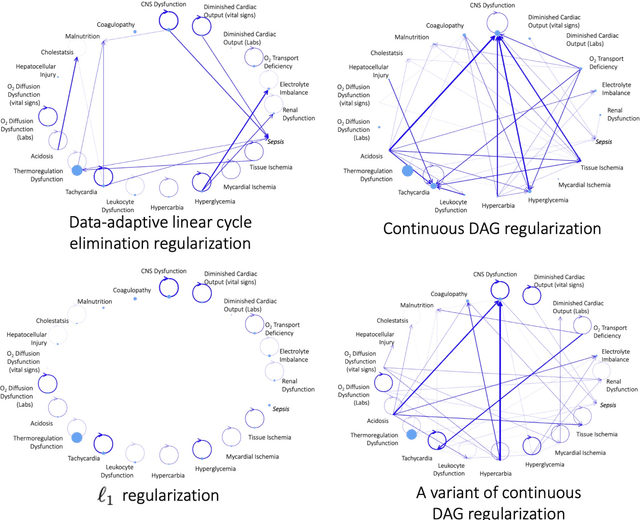
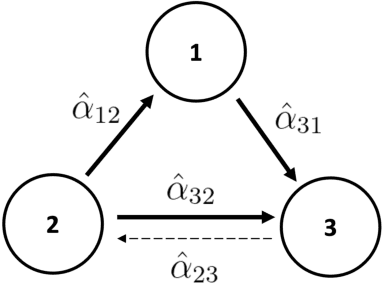
We present a generalized linear structural causal model, coupled with a novel data-adaptive linear regularization, to recover causal directed acyclic graphs (DAGs) from time series. By leveraging a recently developed stochastic monotone Variational Inequality (VI) formulation, we cast the causal discovery problem as a general convex optimization. Furthermore, we develop a non-asymptotic recovery guarantee and quantifiable uncertainty by solving a linear program to establish confidence intervals for a wide range of non-linear monotone link functions. We validate our theoretical results and show the competitive performance of our method via extensive numerical experiments. Most importantly, we demonstrate the effectiveness of our approach in recovering highly interpretable causal DAGs over Sepsis Associated Derangements (SADs) while achieving comparable prediction performance to powerful ``black-box'' models such as XGBoost. Thus, the future adoption of our proposed method to conduct continuous surveillance of high-risk patients by clinicians is much more likely.

Causal Structural Learning from Time Series: A Convex Optimization Approach

Structural learning, which aims to learn directed acyclic graphs (DAGs) from observational data, is foundational to causal reasoning and scientific discovery. Recent advancements formulate structural learning into a continuous optimization problem; however, DAG learning remains a highly non-convex problem, and there has not been much work on leveraging well-developed convex optimization techniques for causal structural learning. We fill this gap by proposing a data-adaptive linear approach for causal structural learning from time series data, which can be conveniently cast into a convex optimization problem using a recently developed monotone operator variational inequality (VI) formulation. Furthermore, we establish non-asymptotic recovery guarantee of the VI-based approach and show the superior performance of our proposed method on structure recovery over existing methods via extensive numerical experiments.

Online Kernel CUSUM for Change-Point Detection

We develop an online kernel Cumulative Sum (CUSUM) procedure, which consists of a parallel set of kernel statistics with different window sizes to account for the unknown change-point location. Compared with many existing sliding window-based kernel change-point detection procedures, which correspond to the Shewhart chart-type procedure, the proposed procedure is more sensitive to small changes. We further present a recursive computation of detection statistics, which is crucial for online procedures to achieve a constant computational and memory complexity, such that we do not need to calculate and remember the entire Gram matrix, which can be a computational bottleneck otherwise. We obtain precise analytic approximations of the two fundamental performance metrics, the Average Run Length (ARL) and Expected Detection Delay (EDD). Furthermore, we establish the optimal window size on the order of $\log ({\rm ARL})$ such that there is nearly no power loss compared with an oracle procedure, which is analogous to the classic result for window-limited Generalized Likelihood Ratio (GLR) procedure. We present extensive numerical experiments to validate our theoretical results and the competitive performance of the proposed method.

Optimal Sub-sampling to Boost Power of Kernel Sequential Change-point Detection

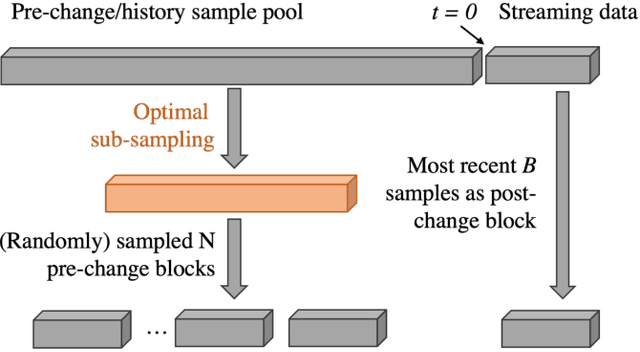
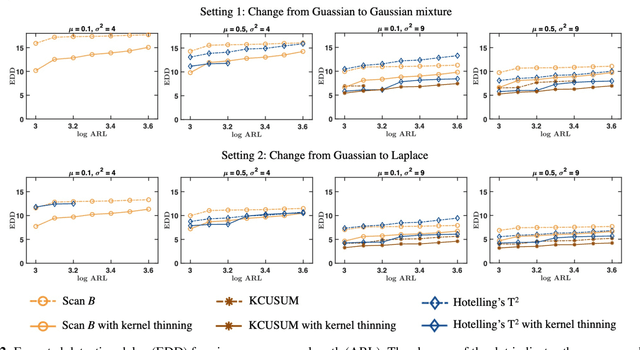
We present a novel scheme to boost detection power for kernel maximum mean discrepancy based sequential change-point detection procedures. Our proposed scheme features an optimal sub-sampling of the history data before the detection procedure, in order to tackle the power loss incurred by the random sub-sample from the enormous history data. We apply our proposed scheme to both Scan $B$ and Kernel Cumulative Sum (CUSUM) procedures, and improved performance is observed from extensive numerical experiments.

Granger Causal Chain Discovery for Sepsis-Associated Derangements via Multivariate Hawkes Processes

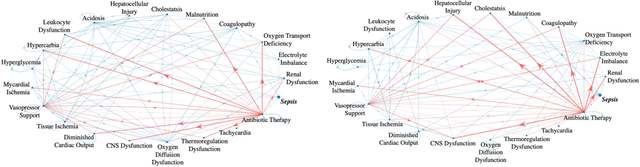
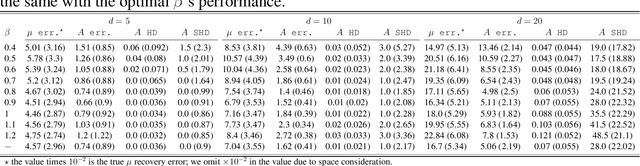
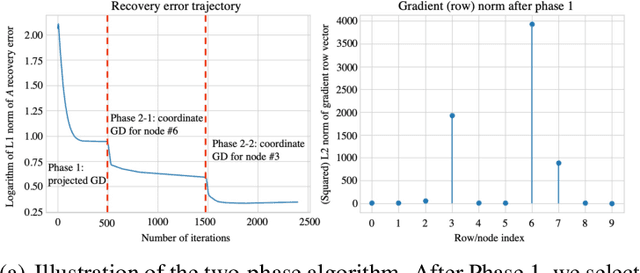
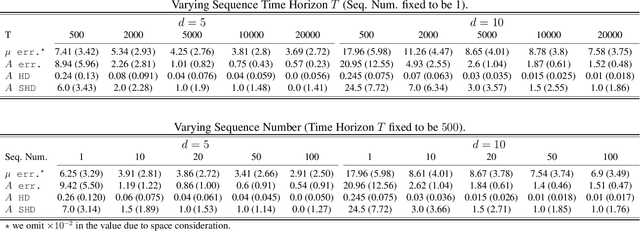
Modern health care systems are conducting continuous, automated surveillance of the electronic medical record (EMR) to identify adverse events with increasing frequency; however, many events such as sepsis do not have clearly elucidated prodromes (i.e., event chains) that can be used to identify and intercept the adverse event early in its course. Currently there does not exist a reliable framework for discovering or describing causal chains that precede adverse hospital events. Clinically relevant and interpretable results require a framework that can (1) infer temporal interactions across multiple patient features found in EMR data (e.g., labs, vital signs, etc.) and (2) can identify pattern(s) which precede and are specific to an impending adverse event (e.g., sepsis). In this work, we propose a linear multivariate Hawkes process model, coupled with $g(x) = x^+$ link function to allow potential inhibition effects, in order to recover a Granger Causal (GC) graph. We develop a two-phase gradient-based scheme to maximize a surrogate of likelihood to estimate the problem parameters. This two-phase algorithm is scalable and shown to be effective via our numerical simulation. It is subsequently extended to a data set of patients admitted to Grady hospital system in Atalanta, GA, where the fitted Granger Causal graph identifies several highly interpretable chains that precede sepsis.

Inferring Granger Causality from Irregularly Sampled Time Series

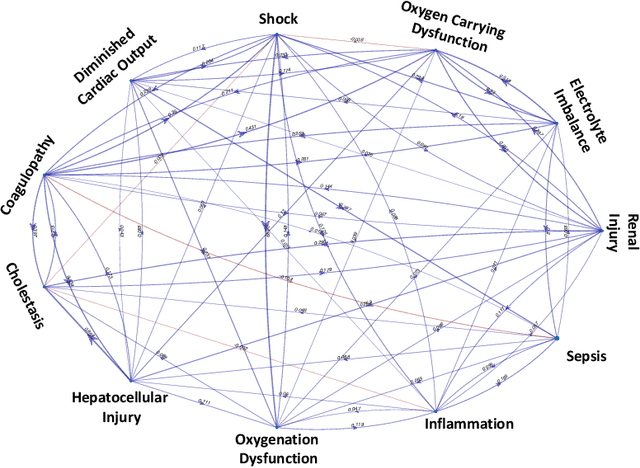
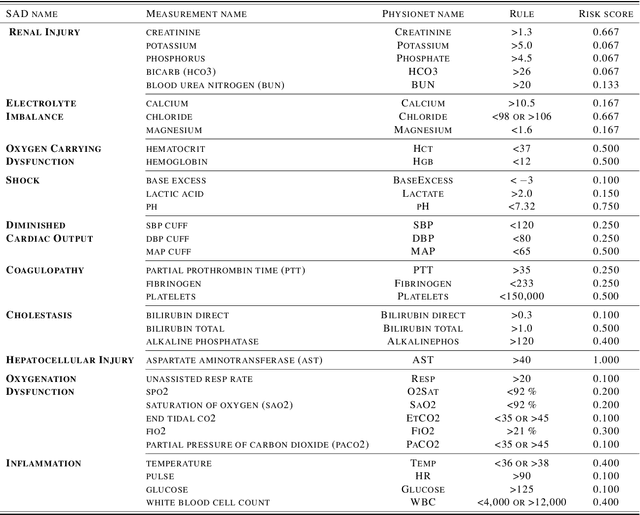
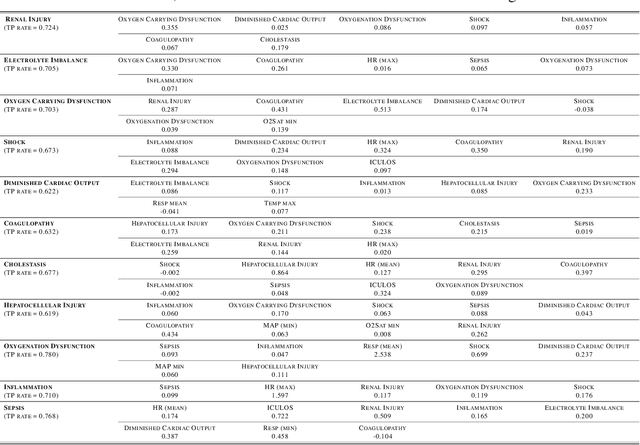
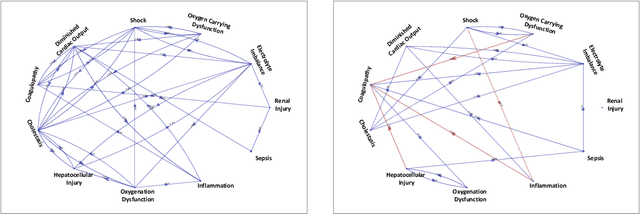
Continuous, automated surveillance systems that incorporate machine learning models are becoming increasingly more common in healthcare environments. These models can capture temporally dependent changes across multiple patient variables and can enhance a clinician's situational awareness by providing an early warning alarm of an impending adverse event such as sepsis. However, most commonly used methods, e.g., XGBoost, fail to provide an interpretable mechanism for understanding why a model produced a sepsis alarm at a given time. The black-box nature of many models is a severe limitation as it prevents clinicians from independently corroborating those physiologic features that have contributed to the sepsis alarm. To overcome this limitation, we propose a generalized linear model (GLM) approach to fit a Granger causal graph based on the physiology of several major sepsis-associated derangements (SADs). We adopt a recently developed stochastic monotone variational inequality-based estimator coupled with forwarding feature selection to learn the graph structure from both continuous and discrete-valued as well as regularly and irregularly sampled time series. Most importantly, we develop a non-asymptotic upper bound on the estimation error for any monotone link function in the GLM. We conduct real-data experiments and demonstrate that our proposed method can achieve comparable performance to popular and powerful prediction methods such as XGBoost while simultaneously maintaining a high level of interpretability.