Causal Graph Discovery from Self and Mutually Exciting Time Series

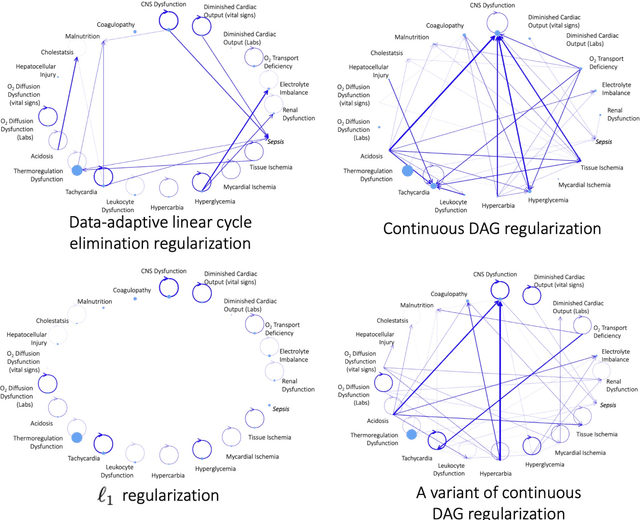
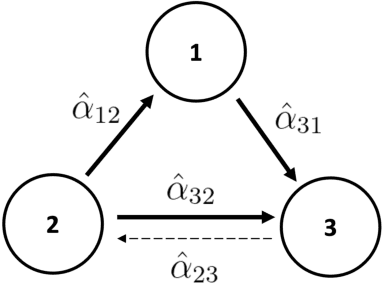
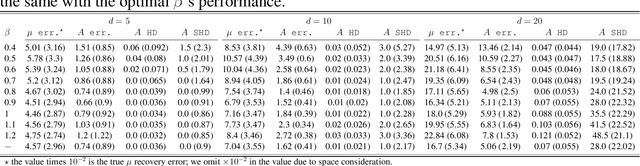
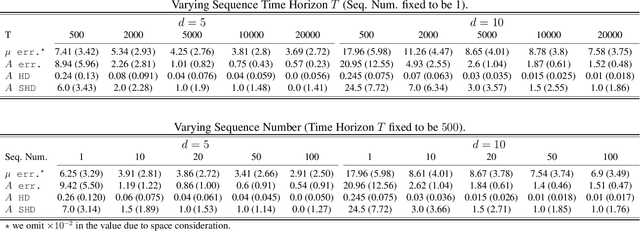
We present a generalized linear structural causal model, coupled with a novel data-adaptive linear regularization, to recover causal directed acyclic graphs (DAGs) from time series. By leveraging a recently developed stochastic monotone Variational Inequality (VI) formulation, we cast the causal discovery problem as a general convex optimization. Furthermore, we develop a non-asymptotic recovery guarantee and quantifiable uncertainty by solving a linear program to establish confidence intervals for a wide range of non-linear monotone link functions. We validate our theoretical results and show the competitive performance of our method via extensive numerical experiments. Most importantly, we demonstrate the effectiveness of our approach in recovering highly interpretable causal DAGs over Sepsis Associated Derangements (SADs) while achieving comparable prediction performance to powerful ``black-box'' models such as XGBoost. Thus, the future adoption of our proposed method to conduct continuous surveillance of high-risk patients by clinicians is much more likely.

Granger Causal Chain Discovery for Sepsis-Associated Derangements via Multivariate Hawkes Processes

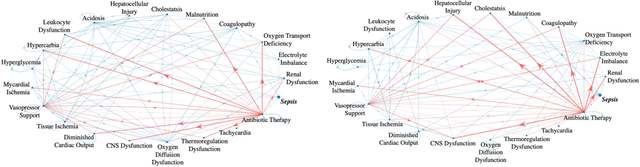
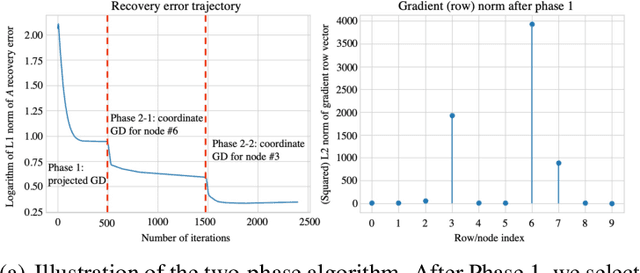
Modern health care systems are conducting continuous, automated surveillance of the electronic medical record (EMR) to identify adverse events with increasing frequency; however, many events such as sepsis do not have clearly elucidated prodromes (i.e., event chains) that can be used to identify and intercept the adverse event early in its course. Currently there does not exist a reliable framework for discovering or describing causal chains that precede adverse hospital events. Clinically relevant and interpretable results require a framework that can (1) infer temporal interactions across multiple patient features found in EMR data (e.g., labs, vital signs, etc.) and (2) can identify pattern(s) which precede and are specific to an impending adverse event (e.g., sepsis). In this work, we propose a linear multivariate Hawkes process model, coupled with $g(x) = x^+$ link function to allow potential inhibition effects, in order to recover a Granger Causal (GC) graph. We develop a two-phase gradient-based scheme to maximize a surrogate of likelihood to estimate the problem parameters. This two-phase algorithm is scalable and shown to be effective via our numerical simulation. It is subsequently extended to a data set of patients admitted to Grady hospital system in Atalanta, GA, where the fitted Granger Causal graph identifies several highly interpretable chains that precede sepsis.

Inferring Granger Causality from Irregularly Sampled Time Series

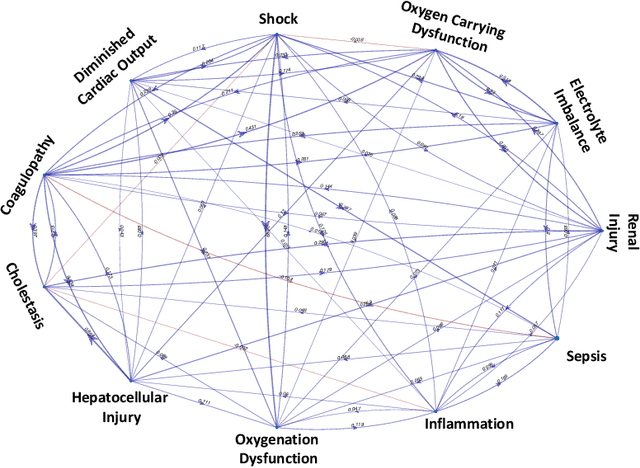
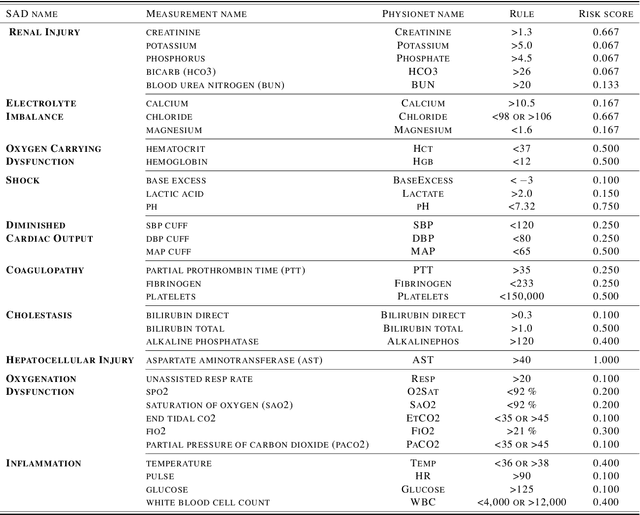
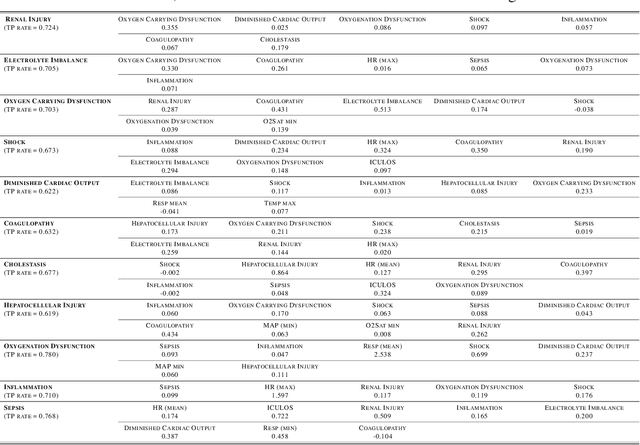
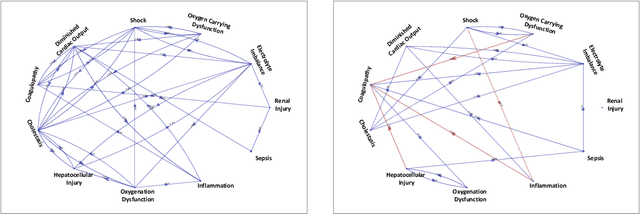
Continuous, automated surveillance systems that incorporate machine learning models are becoming increasingly more common in healthcare environments. These models can capture temporally dependent changes across multiple patient variables and can enhance a clinician's situational awareness by providing an early warning alarm of an impending adverse event such as sepsis. However, most commonly used methods, e.g., XGBoost, fail to provide an interpretable mechanism for understanding why a model produced a sepsis alarm at a given time. The black-box nature of many models is a severe limitation as it prevents clinicians from independently corroborating those physiologic features that have contributed to the sepsis alarm. To overcome this limitation, we propose a generalized linear model (GLM) approach to fit a Granger causal graph based on the physiology of several major sepsis-associated derangements (SADs). We adopt a recently developed stochastic monotone variational inequality-based estimator coupled with forwarding feature selection to learn the graph structure from both continuous and discrete-valued as well as regularly and irregularly sampled time series. Most importantly, we develop a non-asymptotic upper bound on the estimation error for any monotone link function in the GLM. We conduct real-data experiments and demonstrate that our proposed method can achieve comparable performance to popular and powerful prediction methods such as XGBoost while simultaneously maintaining a high level of interpretability.