Factor Importance Ranking and Selection using Total Indices

Factor importance measures the impact of each feature on output prediction accuracy. Many existing works focus on the model-based importance, but an important feature in one learning algorithm may hold little significance in another model. Hence, a factor importance measure ought to characterize the feature's predictive potential without relying on a specific prediction algorithm. Such algorithm-agnostic importance is termed as intrinsic importance in Williamson et al. (2023), but their estimator again requires model fitting. To bypass the modeling step, we present the equivalence between predictiveness potential and total Sobol' indices from global sensitivity analysis, and introduce a novel consistent estimator that can be directly estimated from noisy data. Integrating with forward selection and backward elimination gives rise to FIRST, Factor Importance Ranking and Selection using Total (Sobol') indices. Extensive simulations are provided to demonstrate the effectiveness of FIRST on regression and binary classification problems, and a clear advantage over the state-of-the-art methods.

Rational Kriging

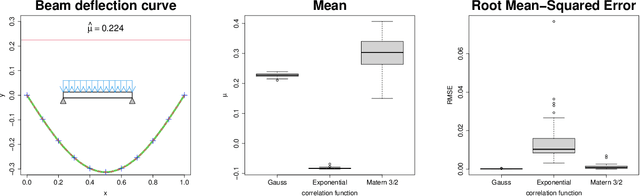
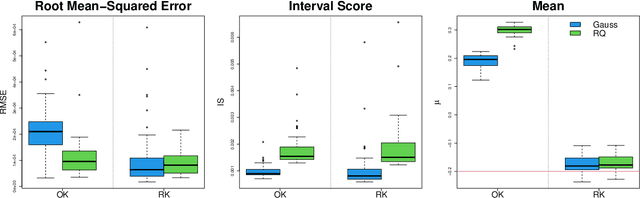
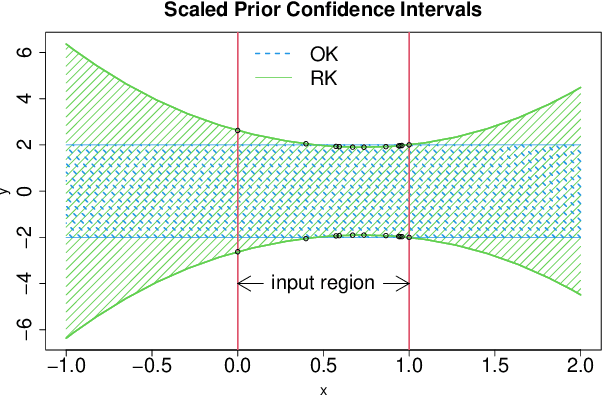
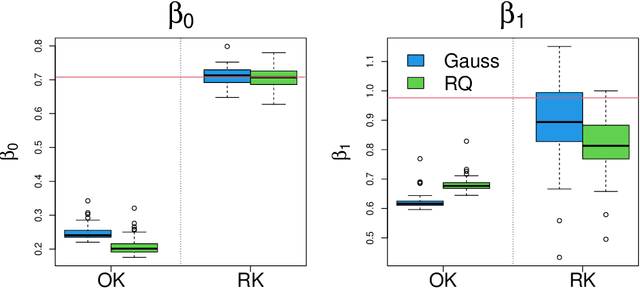
This article proposes a new kriging that has a rational form. It is shown that the generalized least squares estimate of the mean from rational kriging is much more well behaved than that from ordinary kriging. Parameter estimation and uncertainty quantification for rational kriging are proposed using a Gaussian process framework. Its potential applications in emulation and calibration of computer models are also discussed.

Asset Bundling for Wind Power Forecasting

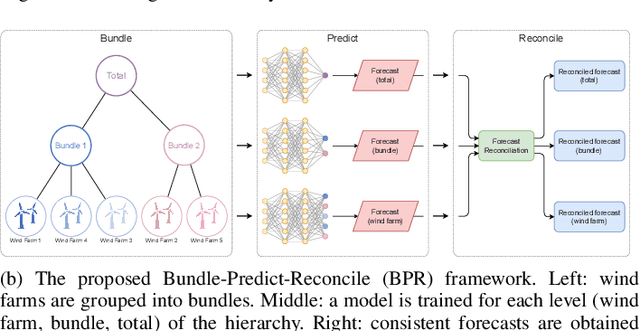
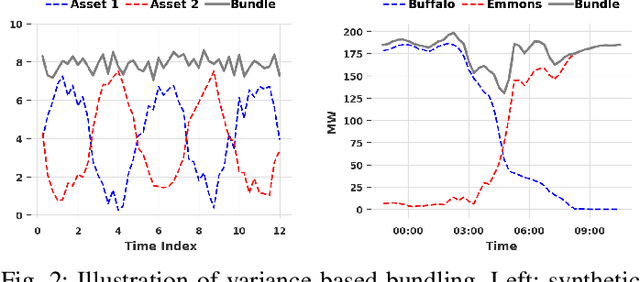
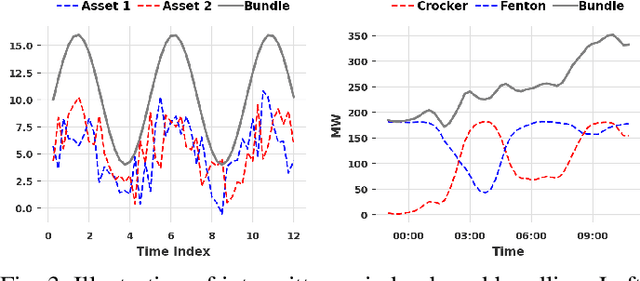
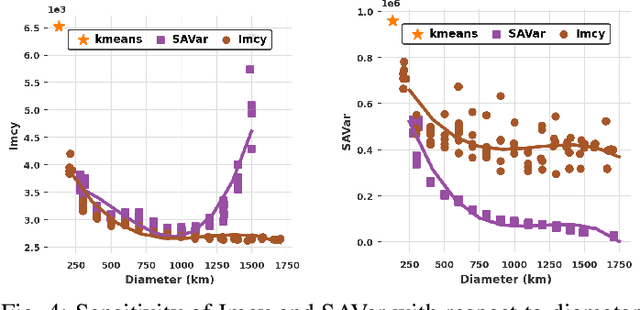
The growing penetration of intermittent, renewable generation in US power grids, especially wind and solar generation, results in increased operational uncertainty. In that context, accurate forecasts are critical, especially for wind generation, which exhibits large variability and is historically harder to predict. To overcome this challenge, this work proposes a novel Bundle-Predict-Reconcile (BPR) framework that integrates asset bundling, machine learning, and forecast reconciliation techniques. The BPR framework first learns an intermediate hierarchy level (the bundles), then predicts wind power at the asset, bundle, and fleet level, and finally reconciles all forecasts to ensure consistency. This approach effectively introduces an auxiliary learning task (predicting the bundle-level time series) to help the main learning tasks. The paper also introduces new asset-bundling criteria that capture the spatio-temporal dynamics of wind power time series. Extensive numerical experiments are conducted on an industry-size dataset of 283 wind farms in the MISO footprint. The experiments consider short-term and day-ahead forecasts, and evaluates a large variety of forecasting models that include weather predictions as covariates. The results demonstrate the benefits of BPR, which consistently and significantly improves forecast accuracy over baselines, especially at the fleet level.

Optimal Ratio for Data Splitting

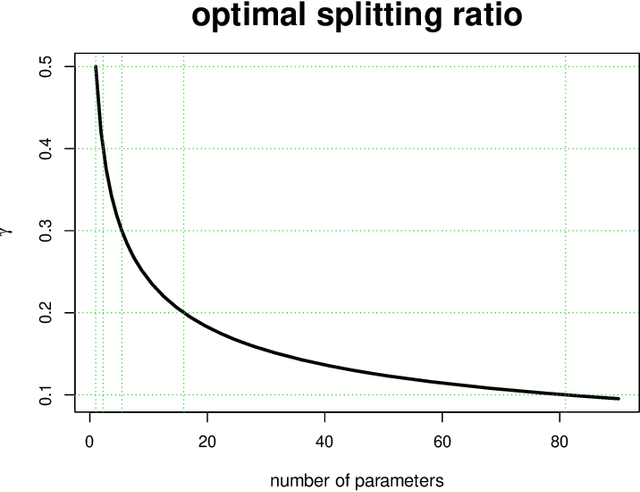
It is common to split a dataset into training and testing sets before fitting a statistical or machine learning model. However, there is no clear guidance on how much data should be used for training and testing. In this article we show that the optimal splitting ratio is $\sqrt{p}:1$, where $p$ is the number of parameters in a linear regression model that explains the data well.

Data Twinning

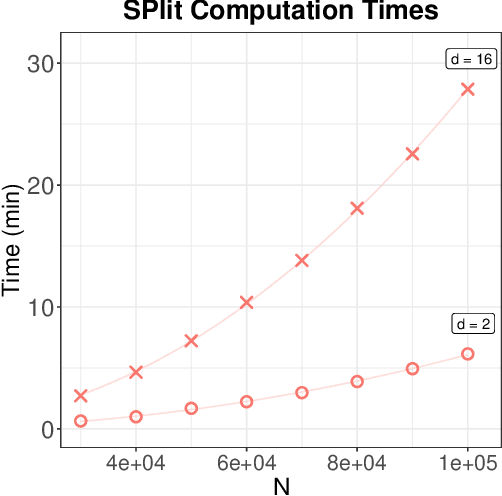
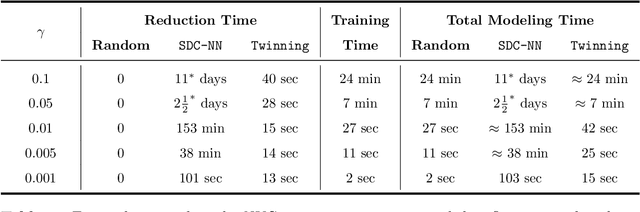
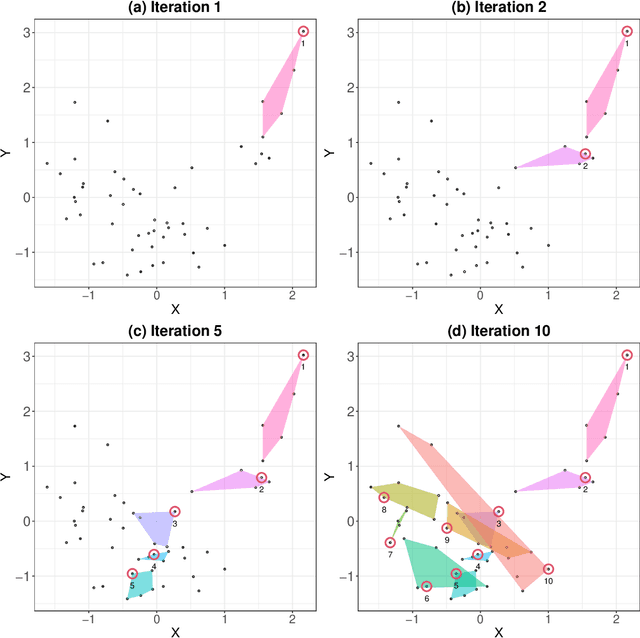
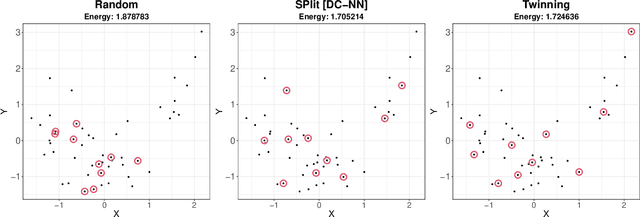
In this work, we develop a method named Twinning, for partitioning a dataset into statistically similar twin sets. Twinning is based on SPlit, a recently proposed model-independent method for optimally splitting a dataset into training and testing sets. Twinning is orders of magnitude faster than the SPlit algorithm, which makes it applicable to Big Data problems such as data compression. Twinning can also be used for generating multiple splits of a given dataset to aid divide-and-conquer procedures and $k$-fold cross validation.

SPlit: An Optimal Method for Data Splitting

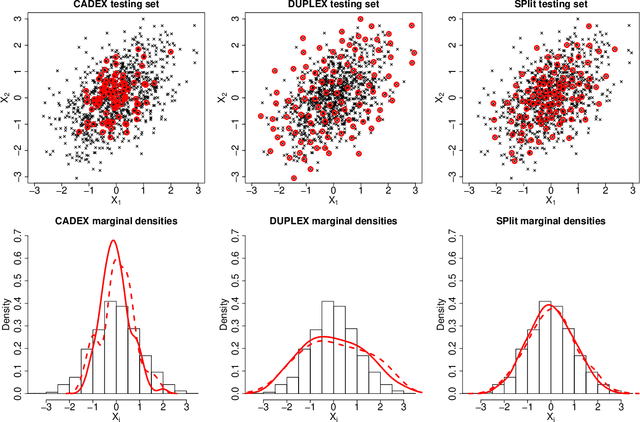
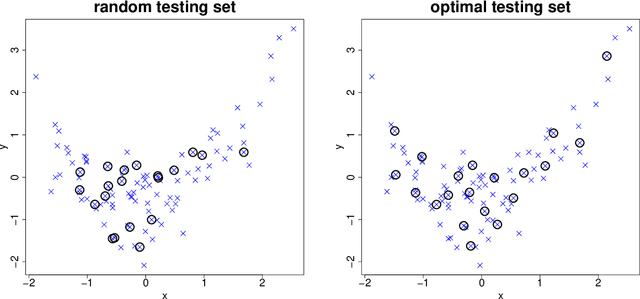
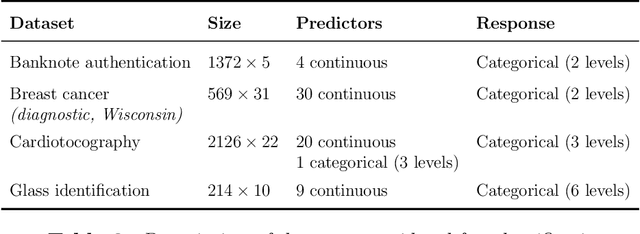
In this article we propose an optimal method referred to as SPlit for splitting a dataset into training and testing sets. SPlit is based on the method of Support Points (SP), which was initially developed for finding the optimal representative points of a continuous distribution. We adapt SP for subsampling from a dataset using a sequential nearest neighbor algorithm. We also extend SP to deal with categorical variables so that SPlit can be applied to both regression and classification problems. The implementation of SPlit on real datasets shows substantial improvement in the worst-case testing performance for several modeling methods compared to the commonly used random splitting procedure.