How well behaved is finite dimensional Diffusion Maps?

Under a set of assumptions on a family of submanifolds $\subset {\mathbb R}^D$, we derive a series of geometric properties that remain valid after finite-dimensional and almost isometric Diffusion Maps (DM), including almost uniform density, finite polynomial approximation and local reach. Leveraging these properties, we establish rigorous bounds on the embedding errors introduced by the DM algorithm is $O\left((\frac{\log n}{n})^{\frac{1}{8d+16}}\right)$. These results offer a solid theoretical foundation for understanding the performance and reliability of DM in practical applications.

Manifold learning: what, how, and why

Manifold learning (ML), known also as non-linear dimension reduction, is a set of methods to find the low dimensional structure of data. Dimension reduction for large, high dimensional data is not merely a way to reduce the data; the new representations and descriptors obtained by ML reveal the geometric shape of high dimensional point clouds, and allow one to visualize, de-noise and interpret them. This survey presents the principles underlying ML, the representative methods, as well as their statistical foundations from a practicing statistician's perspective. It describes the trade-offs, and what theory tells us about the parameter and algorithmic choices we make in order to obtain reliable conclusions.

The decomposition of the higher-order homology embedding constructed from the $k$-Laplacian

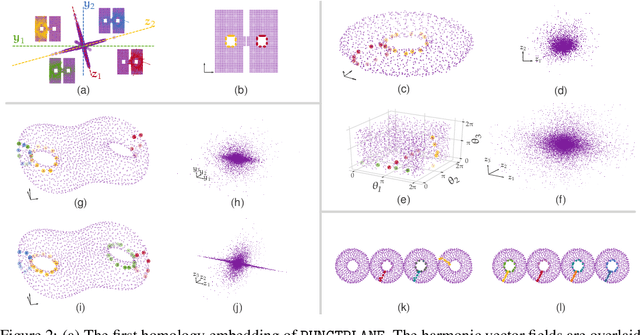
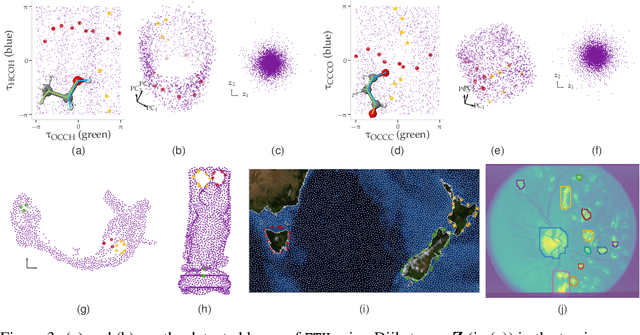
The null space of the $k$-th order Laplacian $\mathbf{\mathcal L}_k$, known as the {\em $k$-th homology vector space}, encodes the non-trivial topology of a manifold or a network. Understanding the structure of the homology embedding can thus disclose geometric or topological information from the data. The study of the null space embedding of the graph Laplacian $\mathbf{\mathcal L}_0$ has spurred new research and applications, such as spectral clustering algorithms with theoretical guarantees and estimators of the Stochastic Block Model. In this work, we investigate the geometry of the $k$-th homology embedding and focus on cases reminiscent of spectral clustering. Namely, we analyze the {\em connected sum} of manifolds as a perturbation to the direct sum of their homology embeddings. We propose an algorithm to factorize the homology embedding into subspaces corresponding to a manifold's simplest topological components. The proposed framework is applied to the {\em shortest homologous loop detection} problem, a problem known to be NP-hard in general. Our spectral loop detection algorithm scales better than existing methods and is effective on diverse data such as point clouds and images.

Distribution free optimality intervals for clustering

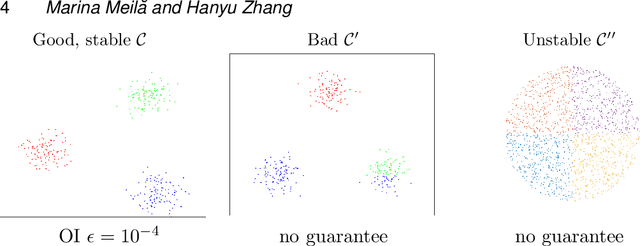
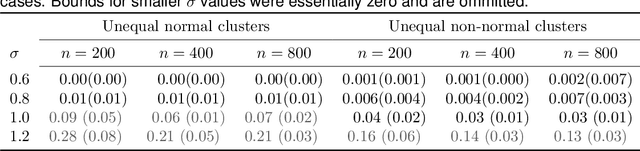
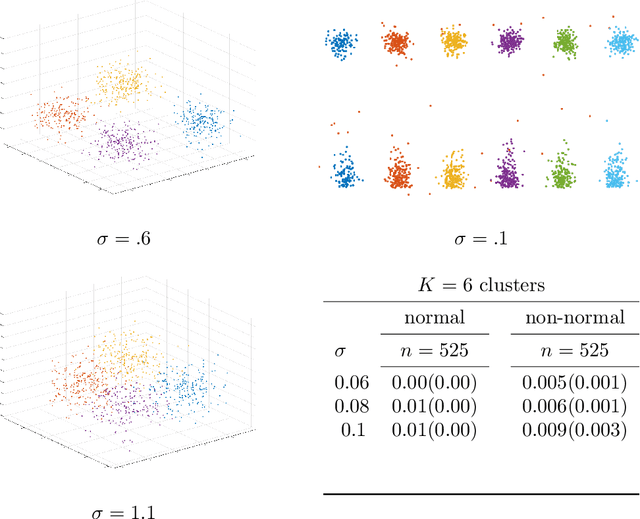
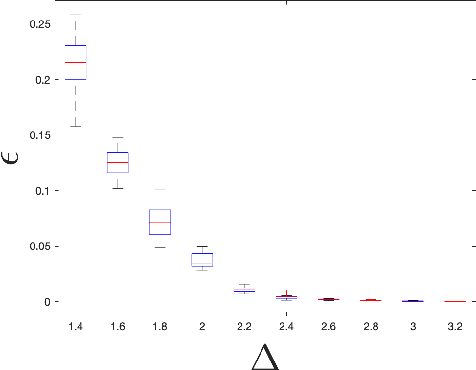
We address the problem of validating the ouput of clustering algorithms. Given data $\mathcal{D}$ and a partition $\mathcal{C}$ of these data into $K$ clusters, when can we say that the clusters obtained are correct or meaningful for the data? This paper introduces a paradigm in which a clustering $\mathcal{C}$ is considered meaningful if it is good with respect to a loss function such as the K-means distortion, and stable, i.e. the only good clustering up to small perturbations. Furthermore, we present a generic method to obtain post-inference guarantees of near-optimality and stability for a clustering $\mathcal{C}$. The method can be instantiated for a variety of clustering criteria (also called loss functions) for which convex relaxations exist. Obtaining the guarantees amounts to solving a convex optimization problem. We demonstrate the practical relevance of this method by obtaining guarantees for the K-means and the Normalized Cut clustering criteria on realistic data sets. We also prove that asymptotic instability implies finite sample instability w.h.p., allowing inferences about the population clusterability from a sample. The guarantees do not depend on any distributional assumptions, but they depend on the data set $\mathcal{D}$ admitting a stable clustering.

Helmholtzian Eigenmap: Topological feature discovery & edge flow learning from point cloud data

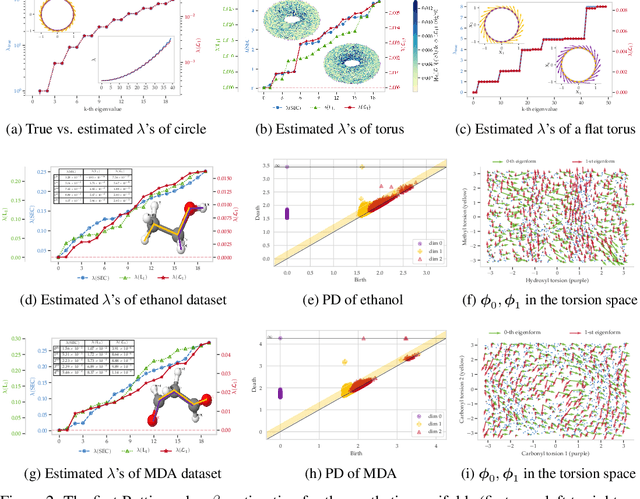
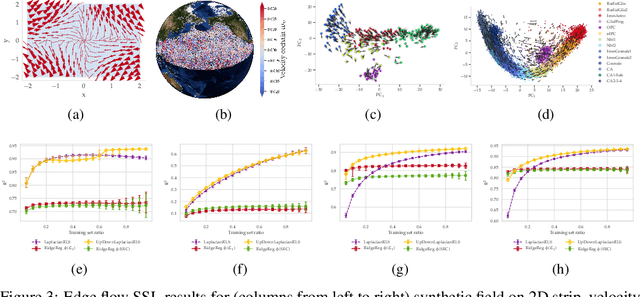
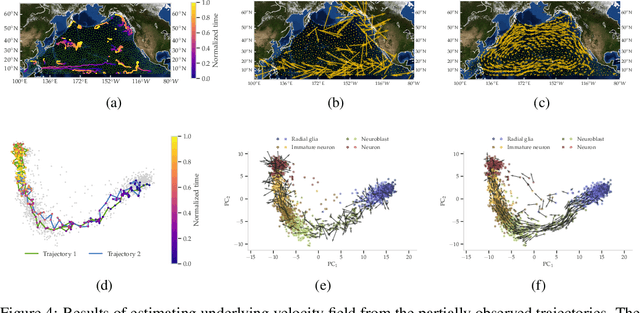
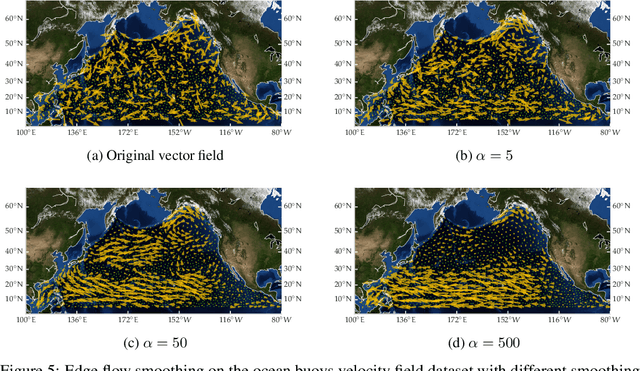
The manifold Helmholtzian (1-Laplacian) operator $\Delta_1$ elegantly generalizes the Laplace-Beltrami operator to vector fields on a manifold $\mathcal M$. In this work, we propose the estimation of the manifold Helmholtzian from point cloud data by a weighted 1-Laplacian $\mathbf{\mathcal L}_1$. While higher order Laplacians ave been introduced and studied, this work is the first to present a graph Helmholtzian constructed from a simplicial complex as an estimator for the continuous operator in a non-parametric setting. Equipped with the geometric and topological information about $\mathcal M$, the Helmholtzian is a useful tool for the analysis of flows and vector fields on $\mathcal M$ via the Helmholtz-Hodge theorem. In addition, the $\mathbf{\mathcal L}_1$ allows the smoothing, prediction, and feature extraction of the flows. We demonstrate these possibilities on substantial sets of synthetic and real point cloud datasets with non-trivial topological structures; and provide theoretical results on the limit of $\mathbf{\mathcal L}_1$ to $\Delta_1$.

Selecting the independent coordinates of manifolds with large aspect ratios

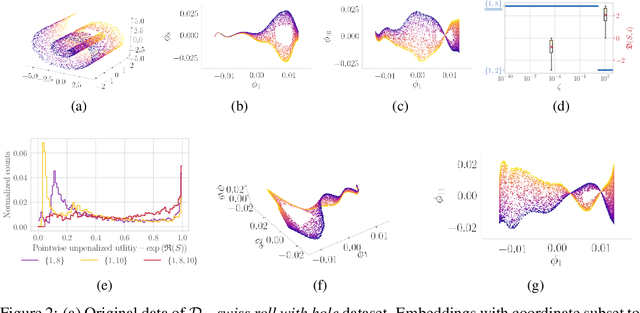
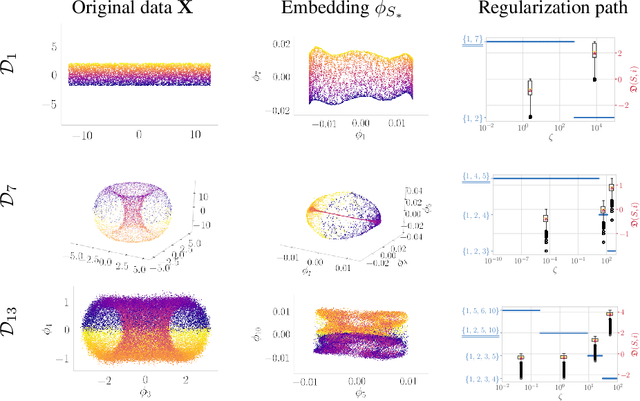
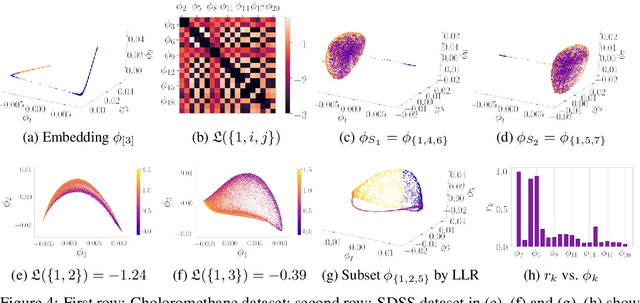
Many manifold embedding algorithms fail apparently when the data manifold has a large aspect ratio (such as a long, thin strip). Here, we formulate success and failure in terms of finding a smooth embedding, showing also that the problem is pervasive and more complex than previously recognized. Mathematically, success is possible under very broad conditions, provided that embedding is done by carefully selected eigenfunctions of the Laplace-Beltrami operator $\Delta$. Hence, we propose a bicriterial Independent Eigencoordinate Selection (IES) algorithm that selects smooth embeddings with few eigenvectors. The algorithm is grounded in theory, has low computational overhead, and is successful on synthetic and large real data.