Improving Generative Ad Text on Facebook using Reinforcement Learning

Generative artificial intelligence (AI), in particular large language models (LLMs), is poised to drive transformative economic change. LLMs are pre-trained on vast text data to learn general language patterns, but a subsequent post-training phase is critical to align them for specific real-world tasks. Reinforcement learning (RL) is the leading post-training technique, yet its economic impact remains largely underexplored and unquantified. We examine this question through the lens of the first deployment of an RL-trained LLM for generative advertising on Facebook. Integrated into Meta's Text Generation feature, our model, "AdLlama," powers an AI tool that helps advertisers create new variations of human-written ad text. To train this model, we introduce reinforcement learning with performance feedback (RLPF), a post-training method that uses historical ad performance data as a reward signal. In a large-scale 10-week A/B test on Facebook spanning nearly 35,000 advertisers and 640,000 ad variations, we find that AdLlama improves click-through rates by 6.7% (p=0.0296) compared to a supervised imitation model trained on curated ads. This represents a substantial improvement in advertiser return on investment on Facebook. We also find that advertisers who used AdLlama generated more ad variations, indicating higher satisfaction with the model's outputs. To our knowledge, this is the largest study to date on the use of generative AI in an ecologically valid setting, offering an important data point quantifying the tangible impact of RL post-training. Furthermore, the results show that RLPF is a promising and generalizable approach for metric-driven post-training that bridges the gap between highly capable language models and tangible outcomes.

The decomposition of the higher-order homology embedding constructed from the $k$-Laplacian

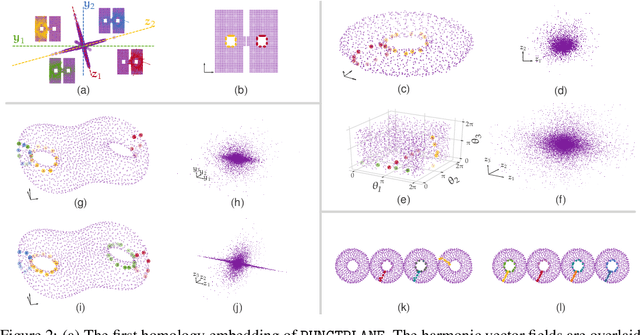
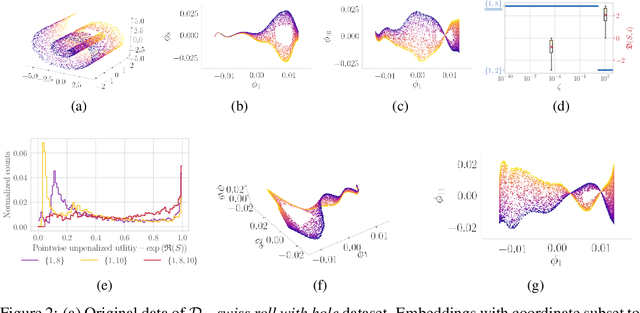
The null space of the $k$-th order Laplacian $\mathbf{\mathcal L}_k$, known as the {\em $k$-th homology vector space}, encodes the non-trivial topology of a manifold or a network. Understanding the structure of the homology embedding can thus disclose geometric or topological information from the data. The study of the null space embedding of the graph Laplacian $\mathbf{\mathcal L}_0$ has spurred new research and applications, such as spectral clustering algorithms with theoretical guarantees and estimators of the Stochastic Block Model. In this work, we investigate the geometry of the $k$-th homology embedding and focus on cases reminiscent of spectral clustering. Namely, we analyze the {\em connected sum} of manifolds as a perturbation to the direct sum of their homology embeddings. We propose an algorithm to factorize the homology embedding into subspaces corresponding to a manifold's simplest topological components. The proposed framework is applied to the {\em shortest homologous loop detection} problem, a problem known to be NP-hard in general. Our spectral loop detection algorithm scales better than existing methods and is effective on diverse data such as point clouds and images.

Helmholtzian Eigenmap: Topological feature discovery & edge flow learning from point cloud data

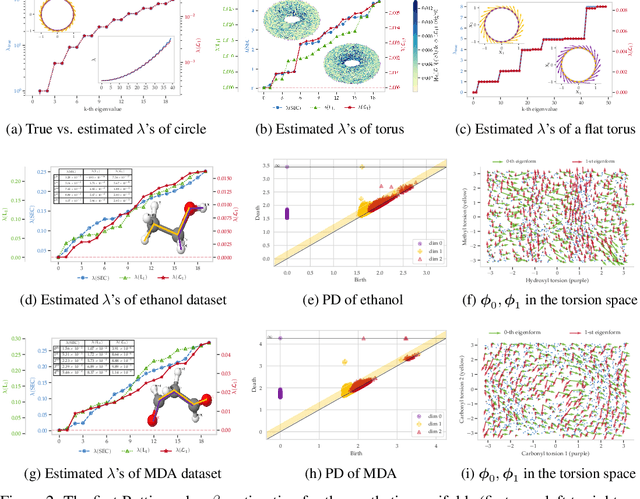
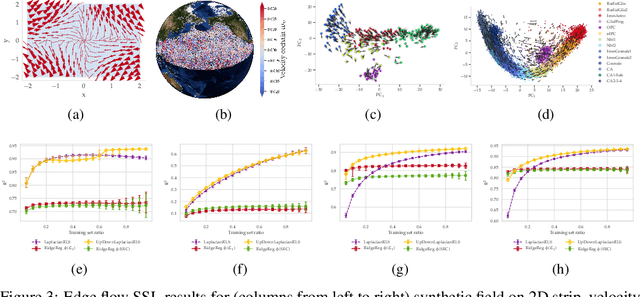
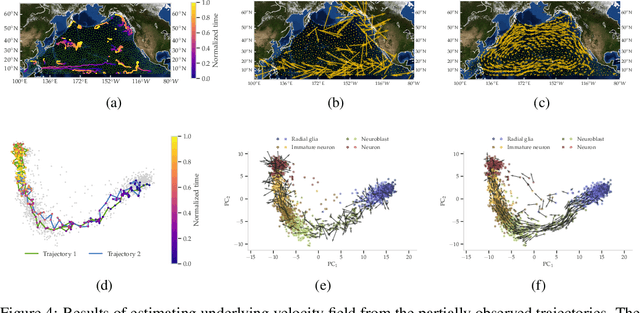
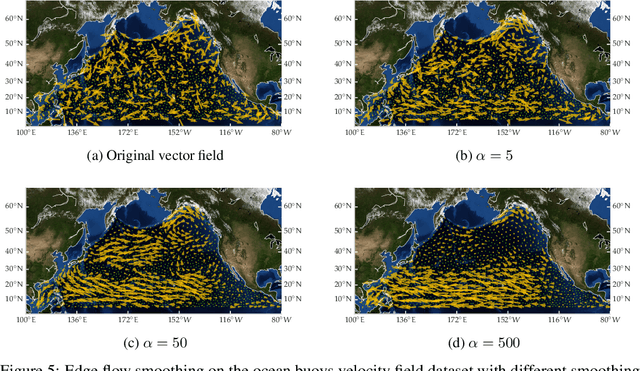
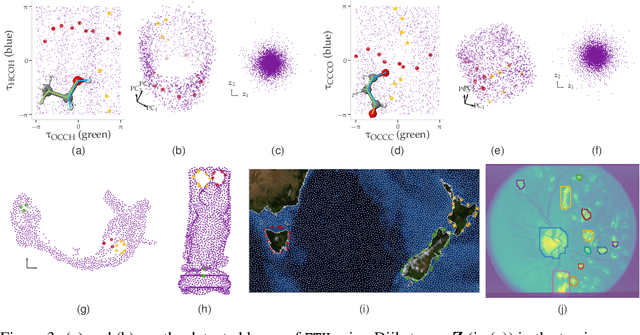
The manifold Helmholtzian (1-Laplacian) operator $\Delta_1$ elegantly generalizes the Laplace-Beltrami operator to vector fields on a manifold $\mathcal M$. In this work, we propose the estimation of the manifold Helmholtzian from point cloud data by a weighted 1-Laplacian $\mathbf{\mathcal L}_1$. While higher order Laplacians ave been introduced and studied, this work is the first to present a graph Helmholtzian constructed from a simplicial complex as an estimator for the continuous operator in a non-parametric setting. Equipped with the geometric and topological information about $\mathcal M$, the Helmholtzian is a useful tool for the analysis of flows and vector fields on $\mathcal M$ via the Helmholtz-Hodge theorem. In addition, the $\mathbf{\mathcal L}_1$ allows the smoothing, prediction, and feature extraction of the flows. We demonstrate these possibilities on substantial sets of synthetic and real point cloud datasets with non-trivial topological structures; and provide theoretical results on the limit of $\mathbf{\mathcal L}_1$ to $\Delta_1$.

Selecting the independent coordinates of manifolds with large aspect ratios

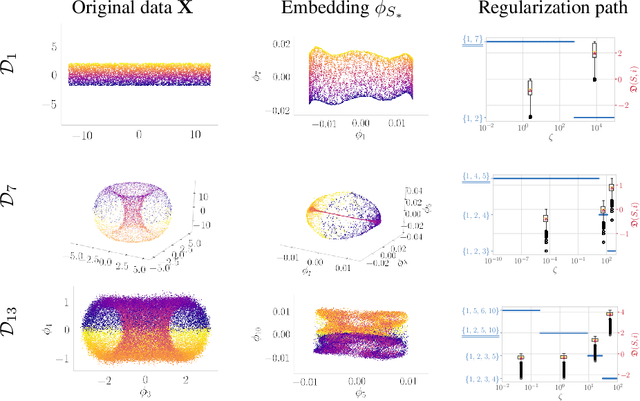
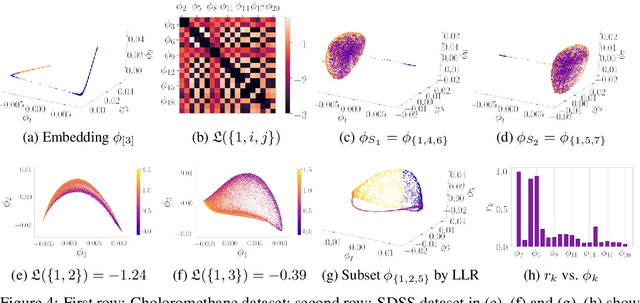
Many manifold embedding algorithms fail apparently when the data manifold has a large aspect ratio (such as a long, thin strip). Here, we formulate success and failure in terms of finding a smooth embedding, showing also that the problem is pervasive and more complex than previously recognized. Mathematically, success is possible under very broad conditions, provided that embedding is done by carefully selected eigenfunctions of the Laplace-Beltrami operator $\Delta$. Hence, we propose a bicriterial Independent Eigencoordinate Selection (IES) algorithm that selects smooth embeddings with few eigenvectors. The algorithm is grounded in theory, has low computational overhead, and is successful on synthetic and large real data.