Helmholtzian Eigenmap: Topological feature discovery & edge flow learning from point cloud data
Paper and Code
Mar 13, 2021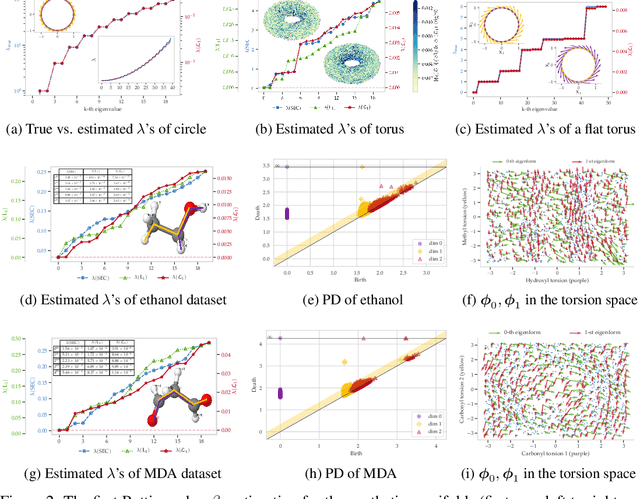
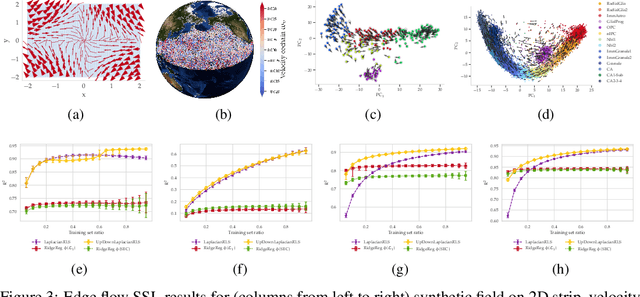
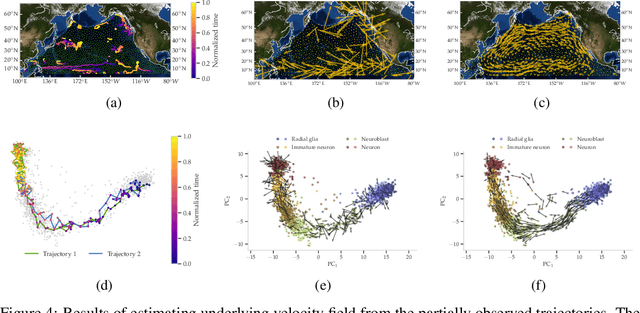
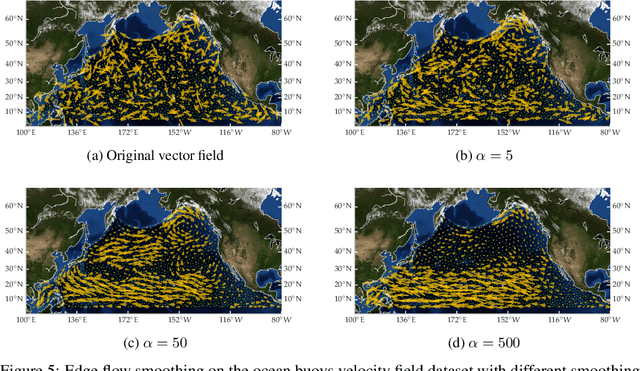
The manifold Helmholtzian (1-Laplacian) operator $\Delta_1$ elegantly generalizes the Laplace-Beltrami operator to vector fields on a manifold $\mathcal M$. In this work, we propose the estimation of the manifold Helmholtzian from point cloud data by a weighted 1-Laplacian $\mathbf{\mathcal L}_1$. While higher order Laplacians ave been introduced and studied, this work is the first to present a graph Helmholtzian constructed from a simplicial complex as an estimator for the continuous operator in a non-parametric setting. Equipped with the geometric and topological information about $\mathcal M$, the Helmholtzian is a useful tool for the analysis of flows and vector fields on $\mathcal M$ via the Helmholtz-Hodge theorem. In addition, the $\mathbf{\mathcal L}_1$ allows the smoothing, prediction, and feature extraction of the flows. We demonstrate these possibilities on substantial sets of synthetic and real point cloud datasets with non-trivial topological structures; and provide theoretical results on the limit of $\mathbf{\mathcal L}_1$ to $\Delta_1$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge